This screenshot gives an equation that will solve for the 2 Semi-Prime factors that make up 2564855351. Yes I know they are already known. It is for proof of concept. Where y equals zero x is the smaller factor of the equation. We graph to reveal (test) this.

I don't understand the error perfectly, but at 41227, the graph should be zero. Mathematically you can plug and chug values and test, but I believe 41227 can be isolated rather fast. So the method is useful and is a step in the right direction for Prime factorization.

Can anyone guide me on how to draw this graph to match what the numbers say is the graph? The graph looks like a barcode and not a one to one graph. It is the same graph I used earlier with a factors of error. In that graph y equaled 0.38 where x was 41227.

If I did not explain this enough, tell me and I will explain further. Thanks.

Thanks for all your help. Are you guessing and checking or is there a function that tells where graphs intersect.

In the Pappy Craylar Conjecture (the last two graphs I posted) the smaller Prime factor occurs when y is between zero and one.

My question is: With the number of values between one and zero. Is the Pappy Craylar Conjecture useful. Obviously Mathematica knows the factor and can factor it in seconds. But if N was larger than what Mathematica could factor would the PCC be useful?

For and N of 2564855351, testing odd values between 50,000 and 41,227 is around 4,000 values. (Note that in the Mathematica Notebooks, I called “N” pnp to prevent conflict.) I can plug in a known x with pnp and it checks, but I cannot solve the equation with knowing pnp alone, because it results in imaginary number values. But are there equations that show the relationships in Prime numbers like the PCC equations do?

And thanks again

Not sure what you mean by

The problem is that more than just the Prime factor come close. I would have to test from 50,000 to 41,000

eq1 = ((x*Sqrt[pnp^3/(pnp*x^2 + x)] + x^4/(pnp^2 + x)) - pnp)
eq2 = (Sqrt[((((x^2*pnp^4 + 2*pnp*x^5) + x^8)/pnp^4)*pnp^2/x^2)] - pnp)

Plot[{eq1, eq2}, {x, 500, 10000},
 PlotRange -> All,
 PlotLabels -> "Expressions"]

FindRoot[eq1 == eq2, {x, 5000}]
(* {x -> 5064.549946} *)

The curves intersect at ~5064.55

Thanks everyone that was extremely helpful. I fixed the one equation. But I was crunching numbers to see why I couldn’t get the graph to intersect. Your corrections say it all. I am getting the two separate graphs to come to 0.2, close at 41,000. But they do not intersect. Is there any class or method that can evaluate when they “almost” intersect?

Why do you think

The should be equal around 41000.

In the domain over which you are plotting the expressions, they are different by 9 orders of magnitude.

ClearAll[x, pnp];
eq1 = ((x*Sqrt[pnp^3/(pnp*x^2 + x)] + x^4/(pnp^2 + x)) - pnp)
eq2 = pnp - (Sqrt[((x^2*pnp^4 + 2*pnp*x^5) + x^8)/pnp^4] - (1 - x^2/(2*pnp)))

pnp = 2564855352;
Plot[{eq1, eq2}, {x, 10000, 50000},
 PlotRange -> All,
 PlotLabels -> "Expressions"]

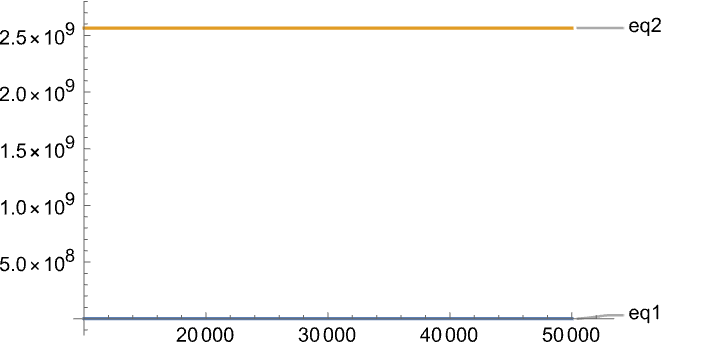
By looking at the two expressions it is clear that they can only be close in magnitude for very large values of x.

Plot[{eq1, eq2}, {x, 9000000, 10000000},
 PlotRange -> All,
 PlotLabels -> "Expressions"]

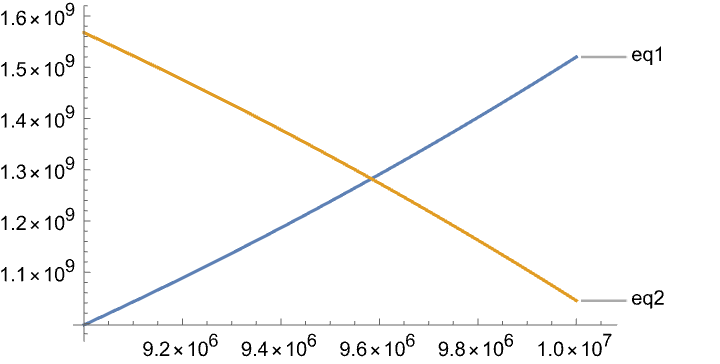
FindRoot[eq1 == eq2, {x, 10000000}, WorkingPrecision -> 10]
(* {x -> 9.583792130*10^6} *)

Which is not ~41000.

WL is case-sensitive, this does nothing and returns unevaluated. Should be Clear.

clear[x, pnp]

Why won't this loop?

clear [i, pnp]

pnp= 2564855351


i=3; while[  ((((pnp^2/i + i^2) / pnp * i) – (i^3/pnp)) << pnp, Print[ii]; i=i+2]

Also in Print[ii], ii is not defined, should probably be Print[i], and the parenthesis are not balanced. With i = 3 the test provided to While fails because of the < condition, perhaps you meant <=.

I'm not sure I entirely understand what you're asking for, but if you want to find where two functions intersect, you might just try using Solve:

f[N_] := x^4/(N^2 + x);
g[N_] := (N^2/x + x^2)/N*x - N;
Solve[f[10] == g[10], x]
(* {{x -> 0}, {x -> 0}, {x -> 0}, {x -> 100/9}} *)

With that you could determine where to focus your plot, or maybe add some visualization that highlights the intersections.

Can you be more specific about what views you want? I guess I don't know what a "real time" graph is. I also don't know what "I need that tools on a regular..." means.