Thank you for pointing this out.

N.B.:

(1). I noticed the related comment here as shown below:

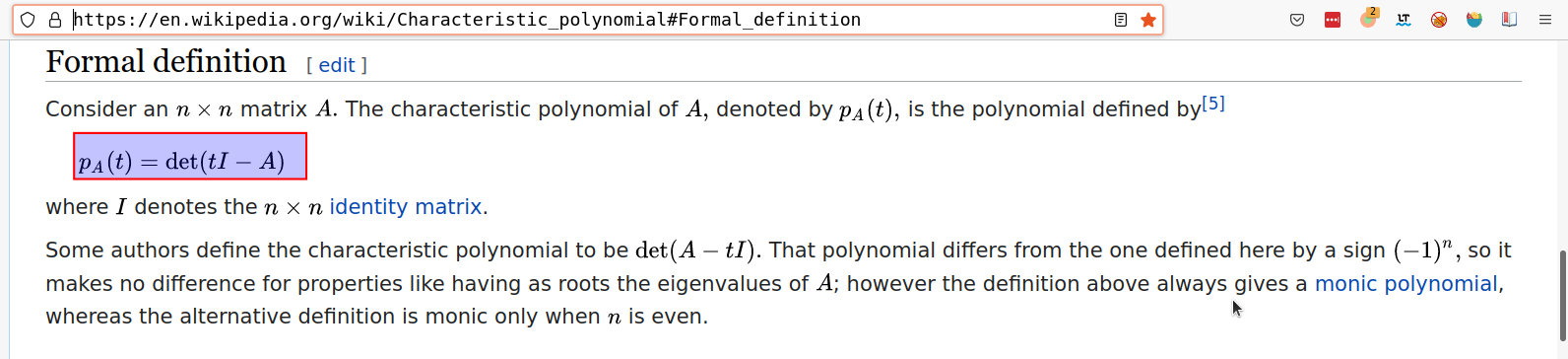
So, although the result is the same, the more appropriate formal definition of this problem should be written as follows:

In[108]:= A="[ [ 0, -1, 0 ], [ 0, 0, -1 ], [ -1, 0, 0 ] ]"//GAP2Wolfram
mat=t IdentityMatrix[3] - A 
{uu, ss, vv} = ResourceFunction["PolynomialSmithDecomposition"][mat]
Diagonal[ss]

Out[108]= {{0, -1, 0}, {0, 0, -1}, {-1, 0, 0}}

Out[109]= {{t, 1, 0}, {0, t, 1}, {1, 0, t}}

Out[110]= {{{0, 0, 1}, {1, 0, -t}, {-t, 1, t^2}}, {{1, 0, 0}, {0, 1, 
   0}, {0, 0, 1 + t^3}}, {{1, 0, -t}, {0, 1, t^2}, {0, 0, 1}}}

Out[111]= {1, 1, 1 + t^3}

(2). I also noticed the following different results given by GAP and the method here.

In GAP:

gap> mat2:=PGGenSet229me3[2];
[ [ -15/4, 29/4, -15/4 ], [ -33/8, 55/8, -25/8 ], [ -25/8, 55/8, -33/8 ] ]
gap> mat2:=mat2*One(x)-x*mat2^0;
[ [ -x-15/4, 29/4, -15/4 ], [ -33/8, -x+55/8, -25/8 ], [ -25/8, 55/8,
-x-33/8 ] ]
gap> d2:=ElementaryDivisorsMat(PolynomialRing(Rationals,1),mat2);
[ 1, 1, x^3+x^2+x+1 ]

The method here:

In[152]:= A="
{{ -15/4, 29/4, -15/4 }, { -33/8, 55/8, -25/8 }, { -25/8, 55/8, -33/8 }}
"//GAP2Wolfram
mat=t IdentityMatrix[3] - A;
{uu, ss, vv} = ResourceFunction["PolynomialSmithDecomposition"][mat];
Diagonal[ss]

Out[152]= {{-(15/4), 29/4, -(15/4)}, {-(33/8), 55/
  8, -(25/8)}, {-(25/8), 55/8, -(33/8)}}

Out[155]= {480, 480, 480 + 480 t + 480 t^2 + 480 t^3}