From your description, I think you need ANCOVA to find the dependence of each answer upon gender and age. Example Link: ANCOVA
For instance, I just want to see the first sheet in your xls:
data = Import["scale.xls", "Sheets" -> "Respuestas de formulario - Tabl"][[1]];
Pick out the categories (from the 2nd colume to the 12th). Use the Part/[[]] function and Span/;; function to extract the title list
In[11]:= title = data[[1,2;;12]]
Out[11]= {A1,A2,A3,A4,A5,A6,A7,A8,A9,AGE,Genero}
Use A1 in the perception table as an example. A1, the second colume: (Use rest to remove the head A1 it self)
In[14]:= a1 = Rest[data[[All,2]]]
Out[14]:= {6.,6.,3.,6.,7.,1.,6.,....,1.,2.}
age:
In[25]:= age = Rest[data[[All,11]]]
Out[25]= {21.,20.,18.,1...,21.}
gender:
In[78]:= gender = Rest[data[[All,12]]]/.{"Femenino "->"F","Masculino"->"M"}
Out[78]= {F,F,F,F,F,F,F,F,F,...,F,M}
Linear model fit for the A1
$A1 = \alpha + \beta D + \gamma x$
where D is the dummy variable/gender and x is a continuous variable/age. You need a ANCOVA/Analysis of Covariance. We need to make the input data in the following form: {gender, age, outcome/A1}
In[80]:= myinput=Transpose[{gender,age,a1}]
Out[80]= {{F,21.,6.},{F,20.,6.},...,{F,19.,1.},{M,21.,2.}}
Use LinearModelFit funciton to find the dependeces:
lm = LinearModelFit[myinput, {DGender, XAge}, {DGender, XAge},NominalVariables -> DGender];
The linear model symbolic expression contains lots of information:
lm["Properties"] // TableForm
including:
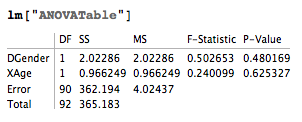
lm["ANOVATable"]
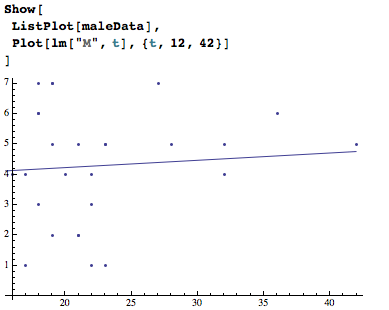
Lets find the data for male customers from 12 to 42.
In[90]:= maleData = Cases[myinput,{"M",__}][[All,2;;]]
Out[90]= {{20.,4.},{23.,5.},{22.,4.},{16.,4.},...,{42.,5.},{21.,2.}}
Use Show, Plot and ListPlot to merge the estimation and raw data points together:
Show[
ListPlot[maleData],
Plot[lm["M", t], {t, 12, 42}]
]
 Attachments:
Attachments: