Many thanks for the reply! Well, giving the working precision in this specific case (up=0.4) did help, but when I increased n or took integration intervals with larger 'up', the problem came back again. Finally I realized that the problem is that the integrand is a product of very small (Exp[...]) and very large (LaguerreL[...]) functions, and precision is lost when calculating the product. So, at large values n and 'up' (what I needed) this is probably an unsolvable problem.

I have found another solution to this problem. Thanks everyone for the replies and reading.

Hello, thanks for the reply! Sorry, my 1st time here. I repeat my question:

Can someone answer my question? I need to integrate a function defined as follow:

bes[x_] := If[x == 0, 1, 2*BesselJ[1, x]/x];
f1[n_, Q_] := Exp[-Q^2/4]*LaguerreL[n - 1, 1, Q^2/4];
f2[n_, Q_] := n*bes[Q*Sqrt[n]];
integrand[n_, Q_] := (f1[n, Q] - f2[n, Q])^2;
result[n_, up_] := NIntegrate[integrand[n, Q], {Q, 0, up}];

In principle, I need the results for n up 100 and the parameter up should be equal to infinity. The integrand is a strongly oscillating function, therefore this is not a simple task. But I get an error message when I ask Mathematica to do a very simple task for me. Here is the result for n=78 and up=0.4:

n = 78;
up = 0.4;
Plot[integrand[n, Q], {Q, 0, up}, PlotRange -> Full]
result[n, up]

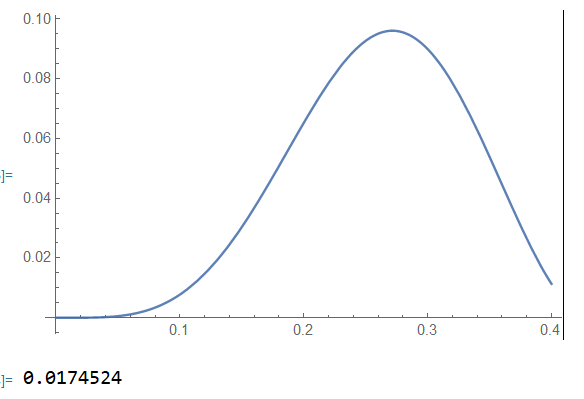
The result 0.01745... looks reasonable. And here is what I get when I try to increase n by one (n=79 and up=0.4):

n = 79;
up = 0.4;
Plot[integrand[n, Q], {Q, 0, up}, PlotRange -> Full]
result[n, up]

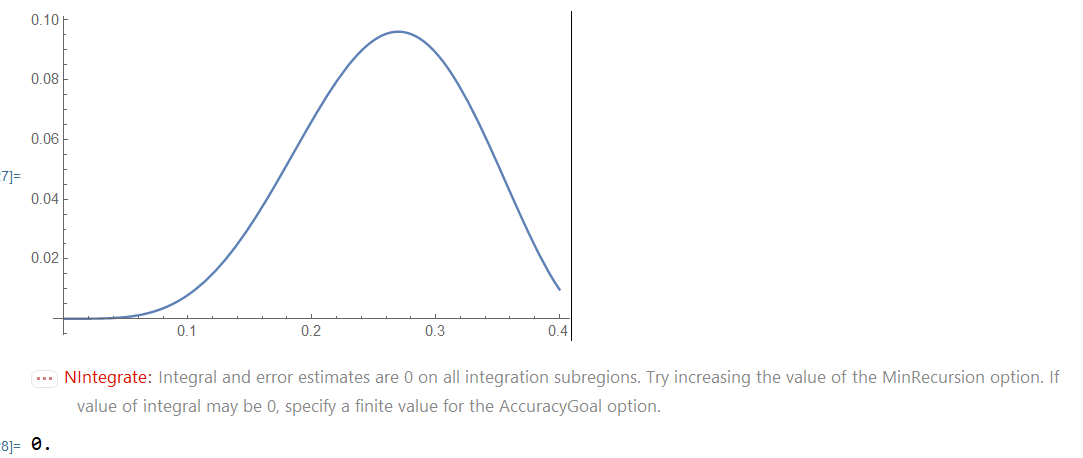
What happens? Plotted are the integrands in both cases; they are quite regular functions. But in the second case Mathematica tells that it cannot integrate such a trivial function and produces the result integral = 0. If I try to increase up, I get the same problem at smaller values of n. Is this a bug in Mathematica? Does someone know, what to do in this case? Many thanks in advance.