I am trying to solve the following Fourier Series problem.

$$f(x)=\begin{cases} -1,& -1<x<0 \newline \;\; 1,&\;\; 0<x<1 \end{cases}$$

We know that on the interval $[-1,1]$ is odd. We calculate the coefficients $$a_0=0 , \quad a_n=0 , \quad b_n=\frac{4}{n\pi}$$

Thus,

$$f(x)= \sum_{n=1}^{\infty} \frac{4}{n\pi} \sin(n \pi x) $$

I tried to study the same problem on Mathematica with the following code

a[n_] := (2/L)*Integrate[f[x]*Cos[2 n*Pi*x/L], {x, -L/2, L/2}]
a[0] := (1/L)*Integrate[f[x], {x, -L/2, L/2}]
b[n_] := (2/L)*Integrate[f[x]*Sin[2 n*Pi*x/L], {x, -L/2, L/2}]
F[x_, N_] := a[0] + Sum[a[n]*Cos[2 n*Pi*x/L] + b[n]*Sin[2 n*Pi*x/L], {n, 1, N}]
p[N_, a_] := 
 Plot[Evaluate[F[x, N]], {x, -a, a}, PlotRange -> All, 
  PlotPoints -> 200]
L=2;
f[x_] = If[x > 0, 1, -1];
a[n]
a[0]
b[n]
Simplify[%, n \[Element] Integers]
Table[F[0.5, k], {k, 0, 20}]

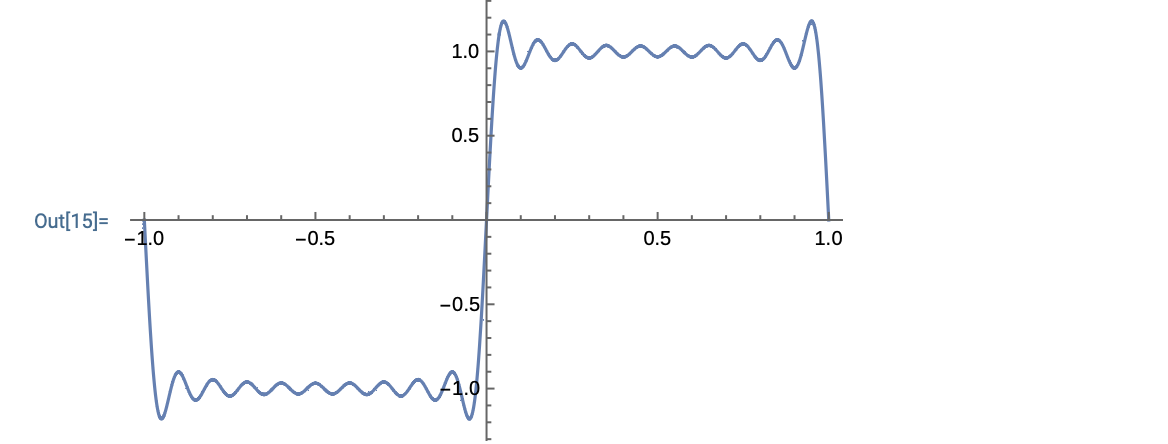
We notice that with the exception of the first value all other values are double. Why is this phenomenon observed? I know that is more a maths question than a Mathematica one but I would appreciate any help.