Hi kind people of the Wolfram Community,

I'm having trouble solving this integral: .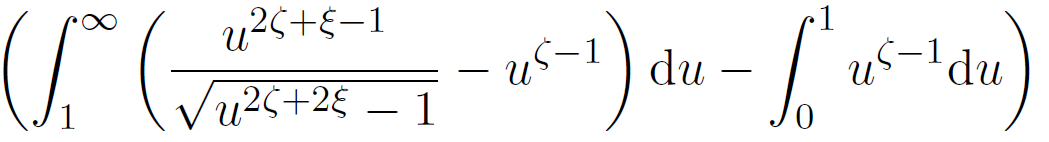

Firstly I do not know how to do this in one calculation, due to the difference in boundary conditions. Secondly there is a more important problem: If I perform the integration on the first part:

  Integrate[(y^(2 a + b - 1)/Sqrt[y^(2 (a + b)) - 1] - y^(a - 1)), {y,   1, Infinity}]

I get the output:

 ConditionalExpression[ 1/a - (Sqrt[\[Pi]]  Gamma[-(a/(2 (a + b)))])/((2 a + b) Gamma[-1 + b/(2 (a + b))]),   Re[2 a + b] > 0 && Re[a] < 0]

So I assume this diverges if not "Re[2 a + b] > 0 && Re[a] < 0". However if I insert a=b=1 then Re[a]>0 and still the integral coverges:

Integrate[(y^(2 + 1 - 1)/Sqrt[y^(2 (2)) - 1] - y^(1 - 1)), {y, 1,  Infinity}]

Output:

1 - EllipticE[-1] + (2 - I) EllipticK[-1] - EllipticK[2]

Or if I NIntegrate I get the value 0.40093.

How do I get an accurate idea of the regions for which this expression converges? And how do I find the solutions in those regions where it does.

I would be very grateful if someone could help me out.

Thanks, M.