I have encountered a problem with Limit function.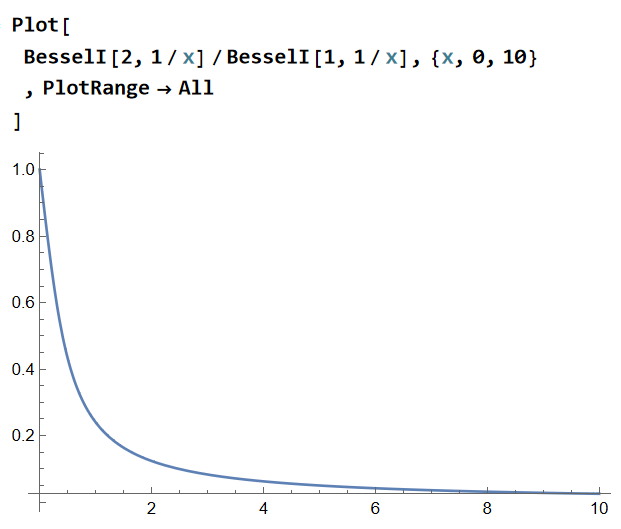

As you can see from the graph, this function is finite in x->+0.

However,

Table[
 Limit[
  FullSimplify[D[BesselI[2, 1/x]/BesselI[1, 1/x], {x, n}]]
  , x -> 0
  , Direction -> "FromAbove"
  ]
 , {n, 1, 6}
 ]

returns

{-(3/2), 3/4, 9/4, 189/16, \[Infinity], 85455/64}

It is obvious that the limit will not be infinite, but Mathematica returns infinity in n=5.

For reference, the true values can be calculated by the following program. (I have not proven that, but probably correct.)

alpha[k_, 
   nu_] := (-1)^k/(k! 8^k) Product[4 nu^2 - (2 i - 1)^2, {i, 1, k}];
alpha[0, nu_] := 1;

delta[k_, nu_, mu_] := 
  alpha[k, mu] - Sum[delta[m, nu, mu] alpha[k - m, nu], {m, 0, k - 1}];
delta[0, nu_, mu_] := 1;

du[k_] := k! delta[k, 1, 2];
du /@ Range[6]

and we will get:

{-(3/2), 3/4, 9/4, 189/16, 405/4, 85455/64}

Is this behavior a bug of Mathematica?

Sorry if there is something wrong with my English.

Regars,