I have encountered a problem with Limit function. 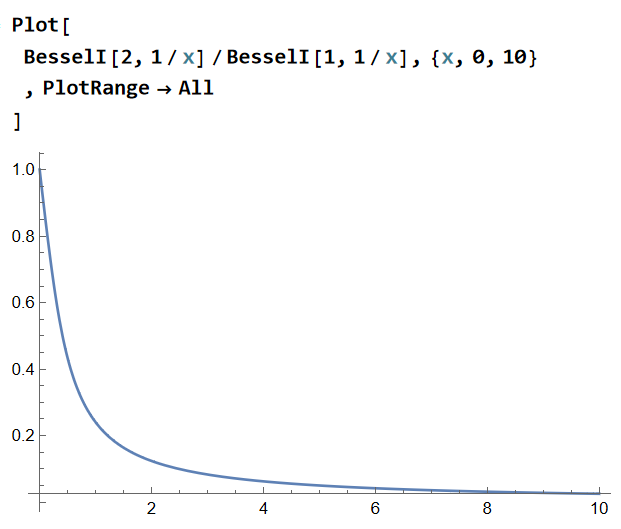
As you can see from the graph, this function is finite in x->+0.
However,
Table[
Limit[
FullSimplify[D[BesselI[2, 1/x]/BesselI[1, 1/x], {x, n}]]
, x -> 0
, Direction -> "FromAbove"
]
, {n, 1, 6}
]
returns
{-(3/2), 3/4, 9/4, 189/16, \[Infinity], 85455/64}
It is obvious that the limit will not be infinite, but Mathematica returns infinity in n=5.
For reference, the true values can be calculated by the following program. (I have not proven that, but probably correct.)
alpha[k_,
nu_] := (-1)^k/(k! 8^k) Product[4 nu^2 - (2 i - 1)^2, {i, 1, k}];
alpha[0, nu_] := 1;
delta[k_, nu_, mu_] :=
alpha[k, mu] - Sum[delta[m, nu, mu] alpha[k - m, nu], {m, 0, k - 1}];
delta[0, nu_, mu_] := 1;
du[k_] := k! delta[k, 1, 2];
du /@ Range[6]
and we will get:
{-(3/2), 3/4, 9/4, 189/16, 405/4, 85455/64}
Is this behavior a bug of Mathematica?
Sorry if there is something wrong with my English.
Regars,