Group Abstract Group Abstract

Message Boards Message Boards

0
|
4.8K Views
|
8 Replies
|
3 Total Likes
View groups...
Share
Share this post:

Improved Eulers Method Problem

It is given the following problem: $$X'=Z+(Y-\alpha)X$$ $$Y'=1-\beta Y-X^2$$ $$Z'=-X-\gamma Z$$ with initial conditions $(X(0),Y(0),Z(0)=(1,2,3)$.

Where

X: interest rate

Υ:investment demand

Z: price index

$\alpha$: savings, $\beta$: cost per investment, $\gamma$: the absolute value of the elasticity of demand

\[Alpha]=0.9;
\[Beta]=0.2;
\[Gamma]=1.2;
f[x_,y_,z_]:=z+(y-\[Alpha])*x
g[x_,y_,z_]:=1-\[Beta]*y-x^2
h[x_,y_,z_]:=-x-\[Gamma]*z

I know how to define a system with two functions so I could use these

  • Method A: accuracy of order h

    S[a_, b_, h_, N_] := (u[0] = a; u[1] = a + h*b; 
Do[u[n + 1] = 
2 u[n] - u[n - 1] + h*h*f[n*h, u[n], (u[n] - u[n - 1])/h], {n, 1, 
N}])

  • Method B: accuracy of order h^2

    Q[a_, b_, h_, N_] := (u[0] = a; v[0] = b; 
    Do[{u[n + 1] = 
    u[n] + h*
    F[u[n] + (h/2)*F[u[n], v[n]], 
    v[n] + (h/2)*
    G[u[n], v[
    n]]],                                                     \

    v[n + 1] = 
    v[n] + h*
    G[u[n] + (h/2)*F[u[n], v[n]], v[n] + (h/2)*G[u[n], v[n]]]}, {n,
    0, N}])
POSTED BY: Athanasios Paraskevopoulos
8 Replies
Sort By:
Rohit Namjoshi
Rohit Namjoshi
Posted 2 years ago

So, initially we have a function with 3 parameters: x, y, and z (f[{x , y , z _}])

No, it is a function that takes a single parameter, which is a List of 3 elements that are locally bound to the symbols x, y, and z.

f[{x_, y_, z_}]

If it took three parameters it would be

f[x_, y_, z_]

This question is unrelated to this thread. You should have asked a new question.
POSTED BY: Rohit Namjoshi

Athanasios,

sorry - obviously I misunderstood your question!

As far as I could understand on the quick the "improved Euler method" I simply would do it like so: 

\[Alpha] = 0.9;
\[Beta] = 0.2;
\[Gamma] = 1.2;

f[{x_, y_, z_}] := {z + (y - \[Alpha])*x, 1 - \[Beta]*y - x^2, -x - \[Gamma]*z}

h = 0.1;
impEuler[v_List] := v + h/2 (f[v] + f[v + h f[v]])

data = NestList[impEuler, {1, 2, 3}, 1000];
Graphics3D[{Arrowheads[{.03, #} & /@ Range[0, 1, .05]], Arrow[data]}, 
 BoxRatios -> Automatic, Axes -> True, AxesLabel -> {"X", "Y", "Z"}]

enter image description here

I do hope that this now is more helpful! At least my "solution" above can be used as reference.

Best regards -- Henrik

POSTED BY: Henrik Schachner

Athanasios,

you did not say so, but I am assuming that you want the above system of DGL get solved:

\[Alpha] = 0.9;
\[Beta] = 0.2;
\[Gamma] = 1.2;

eqs = {x'[t] == z[t] + (y[t] - \[Alpha])*x[t],
   y'[t] == 1 - \[Beta]*y[t] - x[t]^2,
   z'[t] == -x[t] - \[Gamma]*z[t]};

{fx, fy, fz} = NDSolveValue[{eqs, x[0] == 1, y[0] == 2, z[0] == 3}, {x, y, z}, {t, 0, 500}];
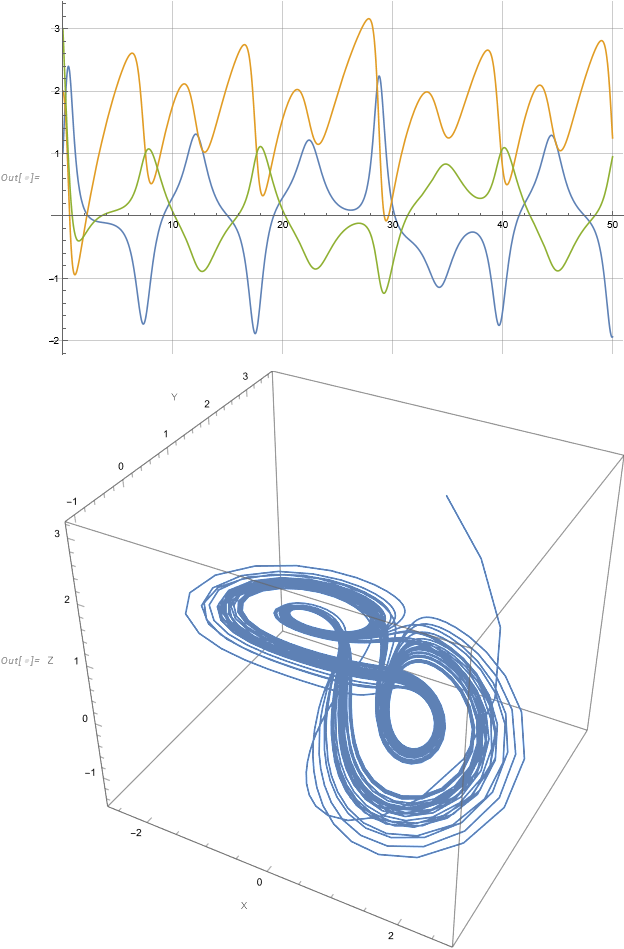
Plot[{fx[t], fy[t], fz[t]}, {t, 0, 50}, ImageSize -> Large, GridLines -> Automatic]
ParametricPlot3D[{fx[t], fy[t], fz[t]}, {t, 0, 500}, ImageSize -> Large, AxesLabel -> {"X", "Y", "Z"}]

enter image description here

I did not know that Euler was dealing with interest rates, etc., but interesting though!

Does that help? Regards -- Henrik
POSTED BY: Henrik Schachner
Cornel B.
Cornel B.
Posted 2 years ago

Hello,

impEuler[v_List] := v + h/2 (f[v] + f[v + h f[v]]) - Henrik Schachner, Radiation Therapy Center, Weilheim, Germany

So, initially we have a function with 3 parameters: x, y, and z (f[{x , y , z _}]), and then we call the function only with one single parameter: v (f[v]). Could you explain what is the meaning of v List, and how f[v] is related to f[{x , y , z }]?

Formula for improved Euler method:

enter image description here enter image description here

POSTED BY: Cornel B.

Another Way I have thought is the following
POSTED BY: Athanasios Paraskevopoulos

That works but it is not accurate as your solution

POSTED BY: Athanasios Paraskevopoulos

Thank you that was very useful for sure. At my master with have an assignment and we study the Dynamic analysis and control of a new hyperchaotic finance system. For this reason we use Improved Euler's Method
POSTED BY: Athanasios Paraskevopoulos

Of course, it helps! But I am trying to use the Improved Euler Method to solve this problem, too
POSTED BY: Athanasios Paraskevopoulos
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard