Hello,
Np = 500;
a = 1;
b = 4.0;
h = (b - a)/Np;
x0 = a;
y[0] = 1;
Y = {{x0, y[0]}};
f[x_, y_] = -y*(x + 1) - Cos[x];
For[m = 0, m <= Np - 1, m++,
xm = a + m*h;
y[m + 1] = y[m] + h*f[xm, y[m]];
AppendTo[Y, {xm + h, y[m + 1]}];
];
g2 = ListLinePlot[Y, PlotStyle -> Green, PlotRange -> All]

Np = 500;
a = 1;
b = 4;
h = (b - a)/Np;
x0 = a;
y[0] = 1;
Y = {{x0, y[0]}};
f[x_, y_] = -y*(x + 1) - Cos[x];
For[m = 0, m <= Np - 1, m++,
xm = a + m*h;
y[m + 1] = y[m] + h*f[xm, y[m]];
AppendTo[Y, {xm + h, y[m + 1]}];
];
g2 = ListLinePlot[Y, PlotStyle -> Green, PlotRange -> All]
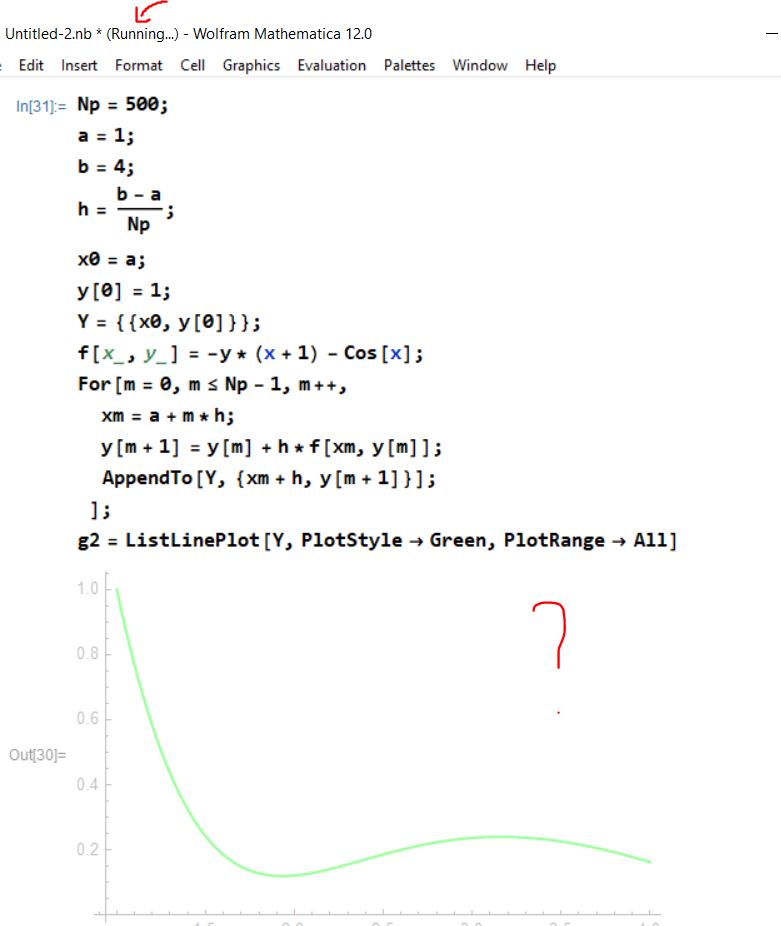
So, the only difference is in b, in that in the first case b=4.0, while in the second case b=4. In the first case the code runs quickly and displays the result, while in the second case, the code runs endlessly and does not display the result.
Can someone explain how exactly that .0 influences the running of the code so much?
Thank you.