Gentlemen...It seems that I managed by myself to put together the code in Mathematica as it should look by comparison with the code in Mathcad, and this is with my little experience of using Wolfram Mathematica.

What is sad is that I thought that I would find more experienced people here in a community of people that use Wolfram Mathematica. I thought I would find the help I needed here in the Wolfram Mathematica community, due to the fact that I assumed I would meet more experienced people here...but it seems that I was wrong in assuming this.

It also seems that I can't really rely on the Wolfram Mathematica community, which in principle shouldn't have been the case (because that's why a community is created, for help). I don't even want to think what I would have done if I had to fight with a more complex code...

Sorry that I had to express these not very pleasant feelings, but...

Also, the code is implemented with for loop...

f[x_, y_] = 1 + y/x + (y/x)^2;
t[0] = 0.;
x[0] = 1.; 
y[0] = 0.;
Subscript[t, start] = t[0];
Subscript[t, final] = 1.;
h = 10^-3;
n = (Subscript[t, final] - Subscript[t, start])/h;
Y1 = {{t[0], x[0]}}; Y2 = {{t[0], y[0]}}; Y3 = {{x[0], y[0]}};

For[i = 0, i \[LessSlantEqual] n-1, i++,
 {
  t[i + 1] = t[i] + h,
  x[i + 1] = x[i] + h,
  y[i + 1] = y[i] + h*f[x[i], y[i]],

  AppendTo[Y1, {t[i + 1], x[i + 1]}],
  AppendTo[Y2, {t[i + 1], y[i + 1]}],
  AppendTo[Y3, {x[i + 1], y[i + 1]}]}]

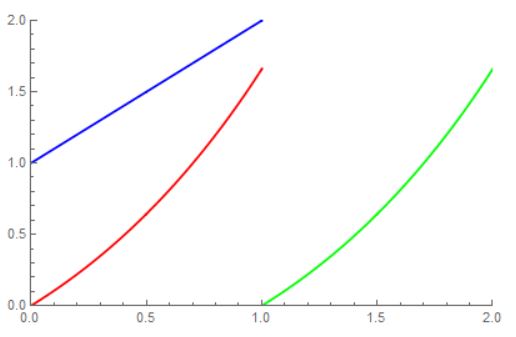
Show[ListLinePlot[Y1, PlotStyle -> Blue, 
  PlotRange -> {{0, 2}, {0, 2}}],    
 ListLinePlot[Y2, PlotStyle -> Red, PlotRange -> {{0, 2}, {0, 2}}], 
 ListLinePlot[Y3, PlotStyle -> Green, PlotRange -> {{0, 2}, {0, 2}}]]

Here is a way to replicate the Mathcad example, using a Do loop inside Module.

f[x_, y_] := 1 + y/x + (y/x)^2

Eu[func_,xinit_,yinit_,tstart_,tfinal_,h_]:=Module[
  {x=xinit,y=yinit,outlist},
  outlist={{tstart,x,y}};
  Do[
    x=x+h//N;
    y=y+h*func[x,y];
    outlist=AppendTo[outlist,{t//N,x,y}],
    {t,tstart+h,tfinal,h}
  ];
  outlist
]

A = Eu[f, 1, 0, 0, 1, 10^(-3)];
Take[A, 12] // Column

Mariusz Iwaniuk,
Henrik Schachner, Radiation Therapy Center, Weilheim, Germany

If even such a thing, as for example the implementation of the Euler method (which is a single equation)), is difficult to implement in Wolfram Mathematica (you don't even find clear examples) and gives you headaches with the implementation, and you must have a very good experience of using Wolfram Mathematica until you manage to implement an equation like the Euler method, then it becomes clear why people choose Mathcad and other software that is more intuitive, easy to use and understand, and which does not give you so much trouble...

Why on earth you would want / insist in using a For[] loop in Mathematica? - Henrik Schachner, Radiation Therapy Center, Weilheim, Germany

As I said in the post, I am also open to other types of implementations that do not necessarily have a For loop in the implementation, but why I keep talking about For is that I have already implemented and tested the respective implementations with For in Matlab (and also in Mathcad, but Matlab is more apropriate in the code to Mathematica than Mathcad - that's why I referred to Matlab), and so I know that this implementation with For loop it works, and on the other hand, having already implemented what I want to implement (for example, this Euler Method) with the For loop in Matlab, I have a reference to follow. But like I said, I'm open to other types of implementations as long as I can understand them.

OK, I would like (to try) to answer the question you asked in this post about a possible implementation of the Euler method in Mathematica. But I think to give an answer here is more appropriate.

To have an example at hand I use the famous Lorenz system. The core of the idea is to do the iteration with NestList[]: say, you want to iterate a function func three times, starting with x0, then you can do it like so:

NestList[func, x0, 3]
(*  Out:  {x0,func[x0],func[func[x0]],func[func[func[x0]]]}   *)

Now for the Euler method on the Lorenz system - here is my approach:

(* function describing v' at time t  -  here Lorenz system: *)
f[{t_, v : {x_, y_, z_}}] := {t, {-3 (x - y), -x z + 26.5 x - y, x y - z}}
(* step size - to be adjusted: *)
h = 0.02;   
(* single step of iteration - general formulation: *)
eulerStep[{t_, v_List}] := {t + h, v + h/2 (f[{t, v}][[2]] + f[{t + h, v + h f[{t, v}][[2]]}][[2]])}
(* initial conditions: *)
init = {0, {0, 1, 0}};
(* performing iteration (here 2000 steps): *)
data = NestList[eulerStep, init, 2000];
pts = Last /@ data;
Graphics3D[{Arrowheads[{.03, #} & /@ Range[0, 1, .05]], Arrow[pts]}, 
 Axes -> True, BoxRatios -> Automatic, AxesLabel -> {"X", "Y", "Z"}]

This reminds me of a washing machine, but in fact it is the well known Lorenz attactor.

Does that help? Regards -- Henrik