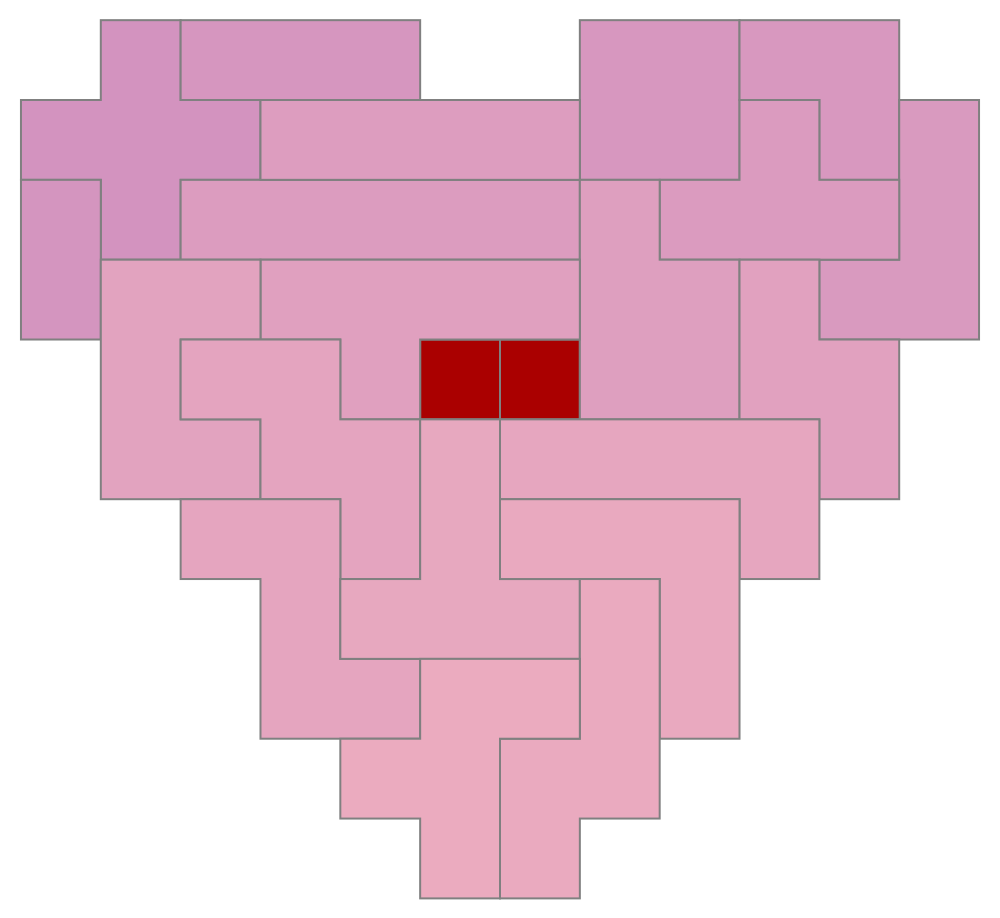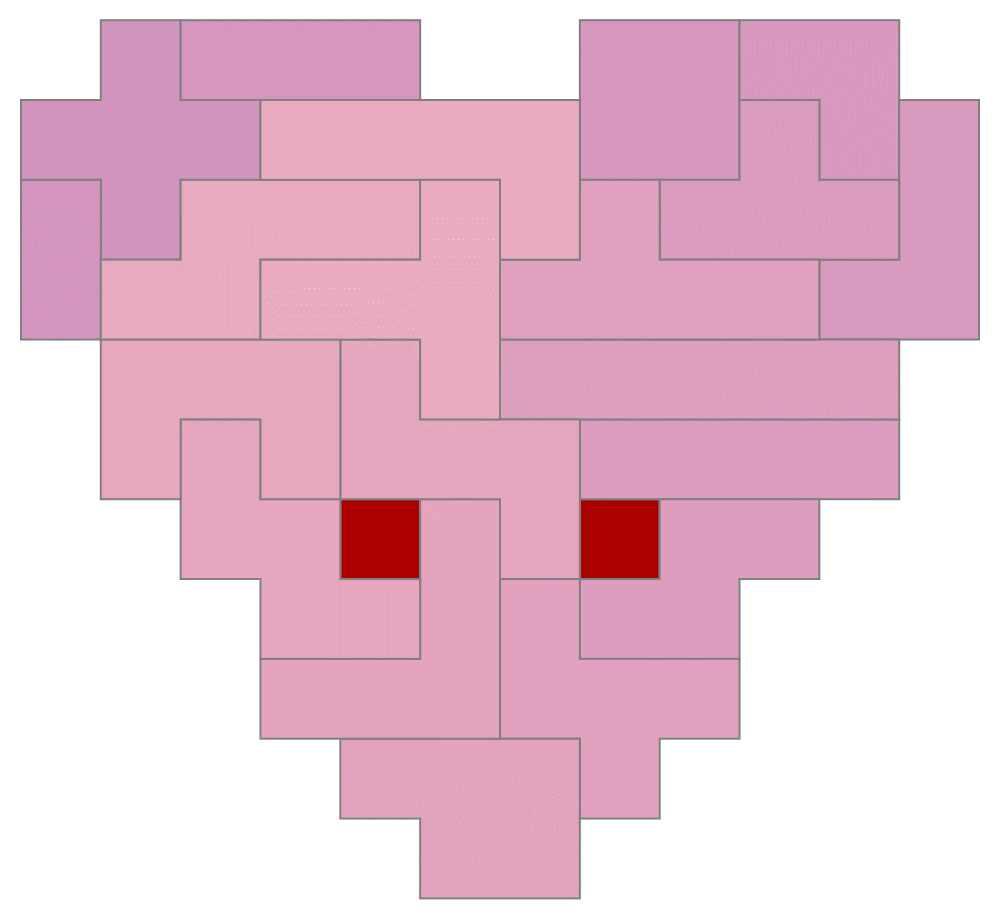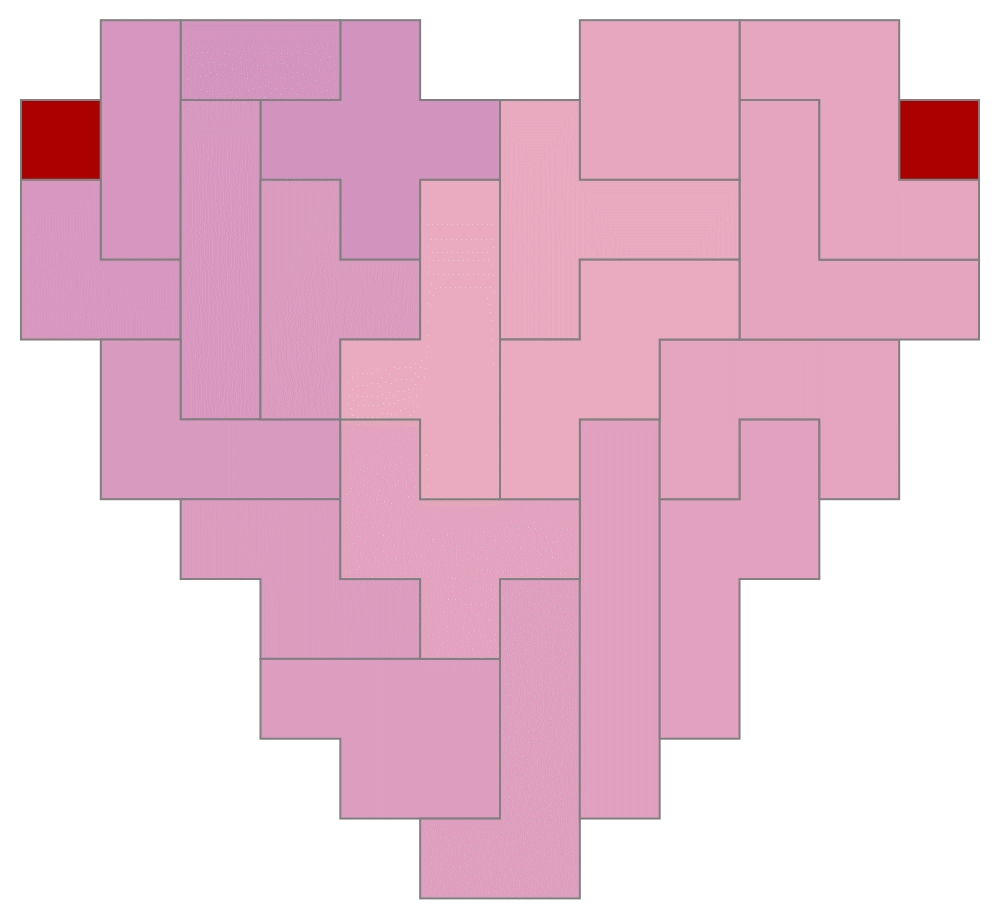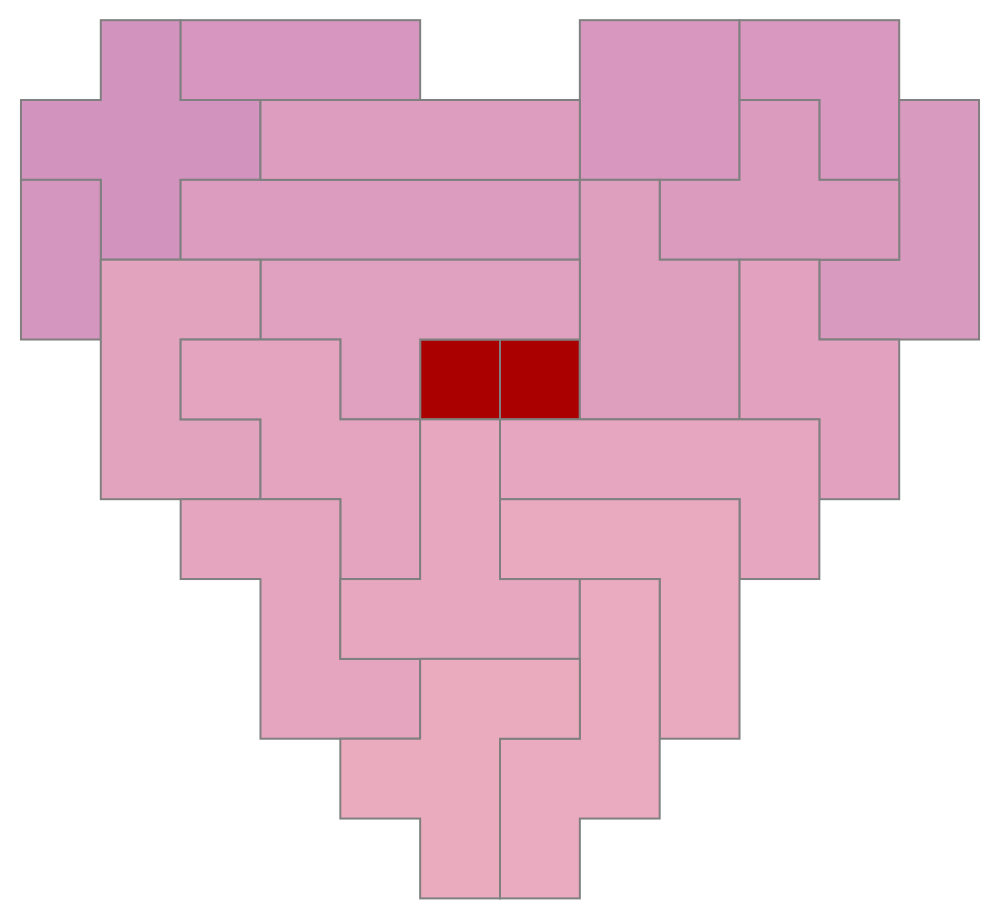
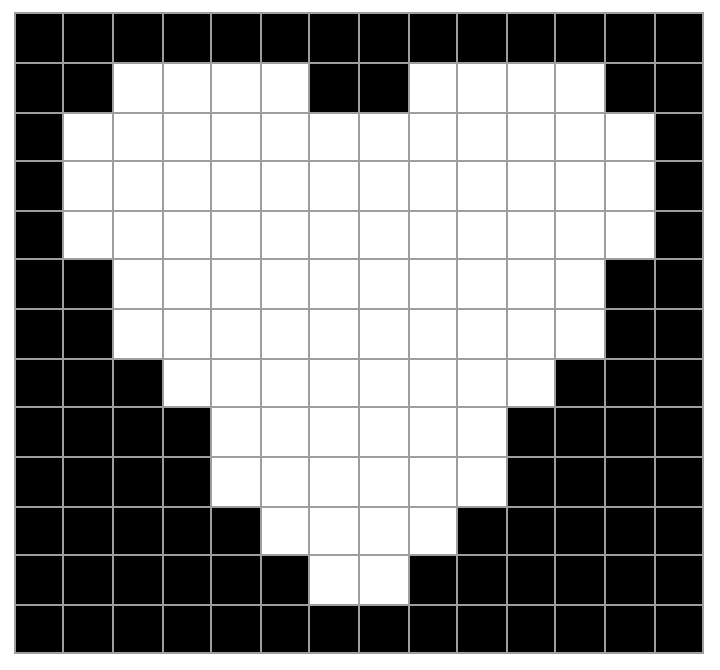
Another year, another heart-shaped holiday to work toward. In this short post, we'll show how to use FindExactCover to find solutions such as seen in the image above.

The domain shape was found by rasterizing the heart text symbol at various font sizes:

heartPixels = Map[Binarize[#*ImageReflect[#, Left]] &[
     ImageCrop[Binarize[Rasterize[Style["♥", #]], .3]]
     ] &, Range[6, 30]];

Labeled[#,
   Count[Catenate[ImageData[#]], 0]
   ] & /@ heartPixels

Right away, the fifth item already looks decently shaped. Since fonts are not very standardized across machines, here I will give the raw data:

heart={
{1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1}, 
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, 
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, 
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, 
{1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1}, 
{1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1}, 
{1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1}, 
{1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1}, 
{1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1}, 
{1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1}, 
{1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1}
}

space= ArrayPad[heart, 1, 1]
ArrayPlot[space, Mesh -> True]]

As in the snowflake example, we are not just looking for a good shape, but also for a happy numerical coincidence where a round sampling of our polyomino lexicon has correct dimensions. In polyomino numerology, the number $$90 = 12 \times 5 + 5 \times 4 +2 \times 3 + 1 \times 2 + 1\times 1+1$$ is almost a round one, but not quite. If we take the $12$ pentominos, the $5$ tetrominos, the $2$ triominos, the $1$ domino and the $1$ monomino, multiply counts by weights and sum, we get 89. Here is one method to generate all 89 shapes as binary Arrays:

ArrayTrim[matrix_] := Transpose[DeleteCases[
   Transpose[DeleteCases[matrix, {0 ..}]], {0 ..}]]

IterateAddSquare[matrix_] := With[{
   newMatrix = ArrayPad[ArrayTrim[matrix], 1],
   pos = Position[ArrayPad[ArrayTrim[matrix], 1], 1]},
  Map[ArrayPad[First[Sort[
       ResourceFunction["ArrayRotations"][
        ArrayTrim[#]]]], 1] &,
   Catenate[Outer[If[
       newMatrix[[Sequence @@ (#1 + #2)]] == 0,
       ReplacePart[newMatrix, #1 + #2 -> 1],
       Nothing] &, pos, ReIm[Exp[I Pi/2 #]
        ] & /@ Range[4], 1]]]]

upToPentominos = Map[ArrayTrim,
   NestList[Union[Catenate[IterateAddSquare /@ #]
      ] &, {ArrayPad[{{1}}, 1]}, 4], {2}];

Dot[Length /@ upToPentominos, Range[5]]

Out[] = 89

A polyomino puzzle with 90 slots could be completed by all polyominos up to weight 5 plus one extra monomino. Again, mathematical purists will likely complaining about the "extra piece". Why should any piece have to be called "extra" on or around St. Valentine's day? No, for now, having just two squares in the puzzle seems very appropriate. It also allows us to tell a visual story with trajectories and state-change dynamics, as in our headliner image.

To put the problem in its standard matrix form we need the function MatricesToCoverMatrix from this earlier post (no one has asked for it at WFR, but now that we're using it again, it still seems like a decent idea for a submission). Given the space and the lexicon, this function will automatically construct a good input for FindExactCover:

pieces = Catenate[upToPentominos[[{1, 1, 2, 3, 4, 5}]]]
heartProblem = MatricesToCoverMatrix[
   space, pieces, "PlaceOne" -> True];
Dimensions@heartProblem
Out[]  = {5328,112}

Once we have this, we can immediately get to finding solutions:

AbsoluteTiming[
 fourRes = ResourceFunction["FindExactCover"][
    heartProblem, 4
    ];]
Out[] ~ 30s 

And for depicting the solutions we need a few more helper functions:

SolutionMatrix[template_, solution_,
  OptionsPattern[{"PlaceOne" -> False}]] := With[
  {len = If[TrueQ[OptionValue["PlaceOne"]],
     Length[solution], 0]}, ReplacePart[template - 1,
   Catenate[MapIndexed[Thread[#1 -> #2[[1]]] &,
     DeleteCases[Times[Position[template, 0], #],
        {0, 0}] & /@ solution[[All, len + 1 ;; -1]]]]]]

IterateSquareJoin[{x_List}] := x
IterateSquareJoin[{x__Integer}] := {x}
IterateSquareJoin[squares_] := Module[
  {first, rest, join, next, int, len},
  first = First[squares];
  rest = Rest[squares];
  join = SelectFirst[rest,
    Length[int = Intersection[First[squares], #]] >= 2 &];
  len = Length[int];
  rest = Complement[rest, {join}];
  join = Reverse[join];
  next = NestWhile[RotateRight, #,
      UnsameQ[Union[#[[1 ;; len]]],
        int] &] & /@ {first, join};
  Prepend[Complement[rest, {join}],
   Join[next[[1, len + 1 ;; -1]], next[[1, {1}]],
    Reverse@next[[2, len + 1 ;; -1]], next[[1, {len}]]]
   ]
  ]

PolyominoPeice[centroids_
  ] := Module[{squares, vertices},
  squares = Outer[Plus, centroids,
    Tuples[{-1, 1}/2, 2][[{1, 2, 4, 3}]], 1];
  vertices = 
   Association[MapIndexed[#1 -> #2[[1]] &, Union @@ squares]];
  squares = Map[vertices[#] &, squares, {2}];
  GraphicsComplex[Keys@vertices, Polygon[
    FixedPoint[IterateSquareJoin, squares]]]
  ]

PolygonDepict[space_, res_, opts : OptionsPattern[{
     ColorFunction -> Automatic,
     EdgeStyle -> Thick, Graphics}]
  ] := Module[{sol, centroids, colFun},
  If[SameQ[colFun = OptionValue[ColorFunction], Automatic],
   colFun = Function[{null}, White]];
  sol = Transpose[
    Reverse[SolutionMatrix[space, res, "PlaceOne" -> True]]];
  centroids = Position[sol, #] & /@ Rest[Union[Flatten[sol]]];
  Graphics[{EdgeForm[OptionValue[EdgeStyle]], MapIndexed[
     {colFun[First[#2]], PolyominoPeice[#1]} &, centroids]},
   FilterRules[{opts}, First /@ Options[Graphics]]]]

The function SolutionMatrix reads raw output FindExactCover and decodes it back into a matrix structure, for example:

SolutionMatrix[space, Last[fourRes], "PlaceOne" -> True] // MatrixForm

The other functions are used to construct polygon polyomino objects wherever the solution matrix has adjacent square elements at equal numerical heights. PolygonDepict accepts a color function, so when making our holiday cards we have a few different options:

GraphicsGrid@Partition[
  PolygonDepict[space, Last[fourRes],
     EdgeStyle -> Directive[Thick, Gray],
     ColorFunction -> #] & /@ {
    Function[Lighter[Red, .9]],
    Function[
     Blend[{Yellow, Orange}, RandomReal[1]]],
    Function[
     Lighter[Hue[#/23], 1/2]],
    Function[
     RandomChoice[Blend[{Purple, Pink},
         #] & /@ Range[0, 1, 1/5]]]
    }, 2]

The last thing we definitely want to do here is to choose the location of the two unit squares. To do so we introduce a filter function which acts on the complete problem encoding:

FilterHeartProblem[heartProblem_, locs_
  ] := Module[{domain, onesloc},
  domain = Position[space, 0];
  onesloc = Flatten[Position[domain, #] & /@ locs];
  If[Or[
      And[#[[1]] == 1, #[[22 + First[onesloc]]] != 1],
      And[#[[2]] == 1, #[[22 + Last[onesloc]]] != 1]
      ], Nothing, # ] & /@ heartProblem
  ]

For example, if we place one square at {6,7} and another at {6,8} then our matrix reduces in size by 178 rows:

reducedProblem = FilterHeartProblem[heartProblem, {{6, 7}, {6, 8}}];
Dimensions[reducedProblem]

Out[]= {5150, 112}

The entire problem can be solved over 90*89/2 = 4005 reduced matrices fixing the unit squares at all possible pairs of locations. There's at least one reason we might want to do so. For animations such as the above (which uses BCA trajectories from the click-to-copy of this recent post), if we have a wide variety of solutions that fix the unit squares in the same place, then we could possibly search the data for smoothest-possible frame transitions. These would involve the least number of pieces changing position from one frame to the next.

We'll put the computation on in the background and see if we can solve any one of the component problems comprehensively. If so then we can estimate how large the space of solutions is, and whether we will be able to effectively calculate all solutions using FindExactCover. Stay tuned!