Hello Eric Rimbey,
I think I managed to do it for Result3 as well
Result3 =
BodePlot[H[I*2*\[Pi]*freq], {freq, 10^-3, 10^6},
PlotRange -> {{-90, 60}, {-180, 0}},
ScalingFunctions -> {{"Log10", "dB"}, {"Log10", "Degree"}},
FrameLabel -> {{HoldForm[Text[Frequency[Hz]]],
HoldForm[Text[Magnitude[dB]]]}, {HoldForm[Text[Frequency[Hz]]],
HoldForm[Text[Phase[Degree]]]}}, GridLines -> Automatic,
FrameTicks -> {{{Automatic,
Automatic}, {Table[{10^i, Superscript[10, i]}, {i, -3, 6}],
None}}, {{Automatic,
Automatic}, {Table[{10^i, Superscript[10, i]}, {i, -3, 6}],
None}}}, PlotStyle -> Thickness[0.01]]
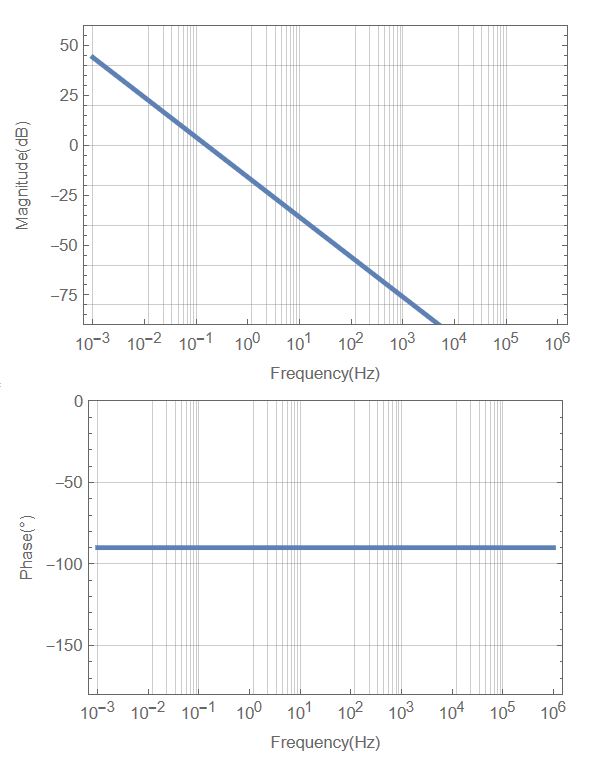
Now the question is related to that Superscript:
Result1 =
BodePlot[H[I*2*\[Pi]*freq], {freq, 10^-3, 10^6},
PlotRange -> {{-90, 60}}, PlotLayout -> "Magnitude",
ScalingFunctions -> {"Log10", "dB"},
FrameLabel -> {HoldForm[Text[Frequency[Hz]]],
HoldForm[Text[Magnitude[dB]]]}, GridLines -> Automatic,
PlotStyle -> Thickness[0.005],
FrameTicks -> {{Automatic,
Automatic}, {Table[{10^i, Superscript[10, i]}, {i, -3, 6}],
None}}]
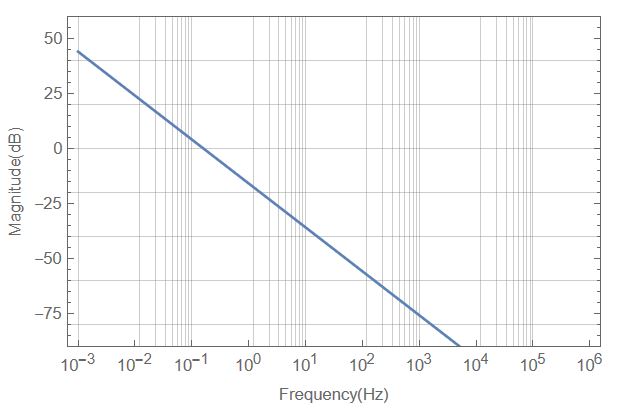
Result4 =
BodePlot[H[I*2*\[Pi]*freq], {freq, 10^-3, 10^6},
PlotRange -> {{-90, 60}}, PlotLayout -> "Magnitude",
ScalingFunctions -> {"Log10", "dB"},
FrameLabel -> {HoldForm[Text[Frequency[Hz]]],
HoldForm[Text[Magnitude[dB]]]}, GridLines -> Automatic,
PlotStyle -> Thickness[0.005],
FrameTicks -> {{Automatic,
Automatic}, {Table[{10^i, 10^i}, {i, -3, 6}], None}}]
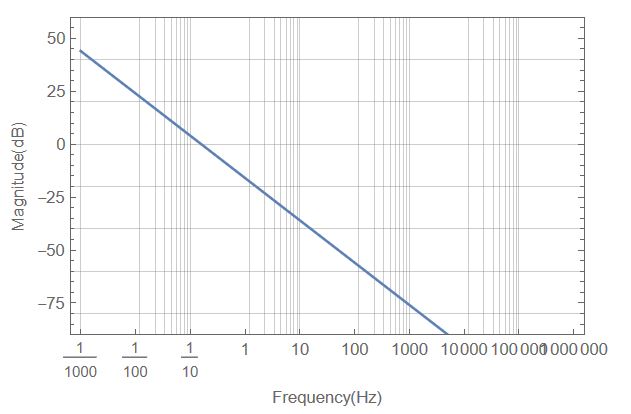
The only difference between Result1 and Result4 is only there in Table[...]
Looks like Superscript[10, i] wouldn't equal 10^i...?
Although it seems that the 2 should have been equal, at least that's what the documentation shows:
https://reference.wolfram.com/language/ref/Superscript.html
Mathematica 13.2 Notebook fille attached.
Thank you.
 Attachments:
Attachments: