Link to the problem: Click here
- Determine the least real number M such that the inequality $ \big|\ ab(a^{2}-b^{2})+bc(b^{2}-c^{2})+ca(c^{2}-a^{2}) \ \big| \leq M \left( a^{2}+b^{2}+c^{2} \right)^{2}$ holds for real number $a, b$ and $c$
IMO algebraic problems are challenging and ugly in many cases when elementary math skill is required to expand, factorize and use AM-GM inequality to progress along the right direction of greater/less sign. I would like to use Wolfram Language to show beautiful side of solving this problem.
The inequality can be interpreted in this way: for all $a, b ,c $, the maximum value on the lhs can never pass the product of $M$ and the square sum of $a,b,c$. If I fix the square sum to $r^2 = a^2 + b^2 +c^2$, then $M\ r^2$ is the maximum value of the rhs.
The manifold/surface of the constant square sum for $a, b$ and $c$ is naturally a sphere of radius $r$. Thus I choose to use spherical coordinate to parametrize the $lhs$ of the inequality:
f[a_, b_, c_] = a*b (a^2 - b^2) + b*c (b^2 - c^2) + c*a (c^2 - a^2)
and the inequality becomes $f(a,b,c) < M r^4$. Let $a = r \cos(\theta)\cos(\phi), b = r \sin(\theta)\cos(\phi), c = \sin(\phi) $, $f(a,b,c)$ becomes:
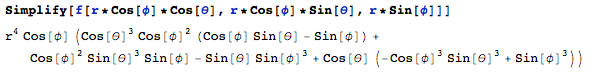
Note that I can cancel the $r^4$ on the both sides and leave $M$ to be possible maximum value of $g(\theta,\phi)$:
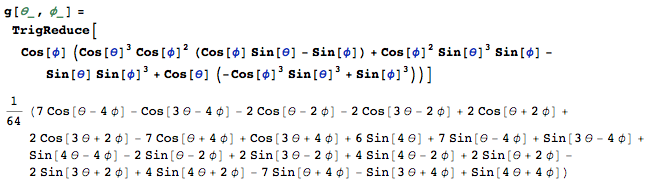
A good thing about analysis and more abstract math is that you only need to care about whether the function is convergent, bounded and smooth. If these beautiful properties are satisfied, simple numeric scheme just work as charm in general. $g(. \ ,\ .)$ is simply a linear combination of the sin/cos function, it is bounded, smooth and periodic.
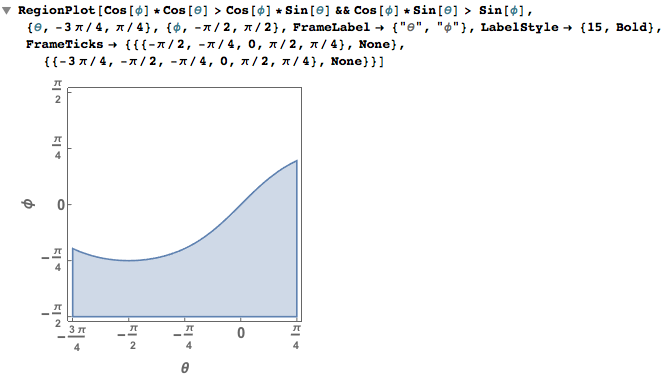
Without loss of generality, I assume $a> b >c$. On the spherical coordinate, we shall have a quite complicated contour to wrap the region:
I also map the region back to the unit sphere, I obtain:

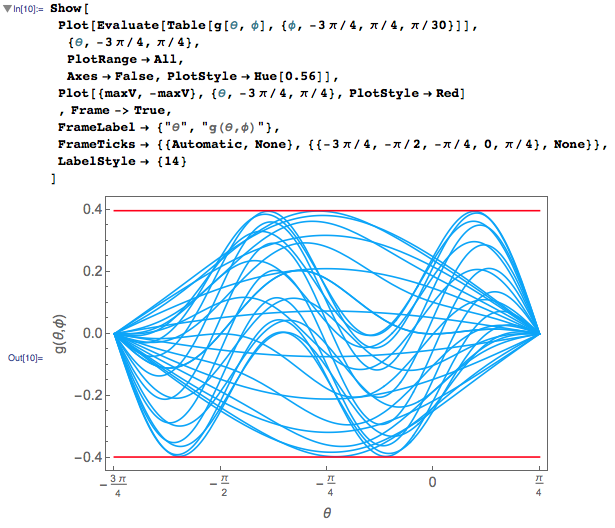
To illustrate the surface formed by $g(\theta,\phi)$, I put the "known" max/min value together with this surface in the plot:

The following grid shows 3 perspective of the waffle:
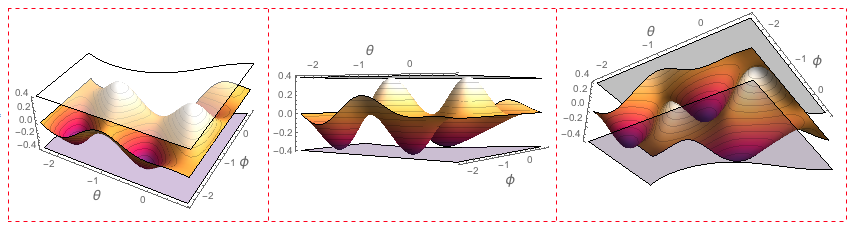
the top and bottom plate hold the lasagna tightly.
Recall the inequality at the very beginning of the thread, there was a $abs$ sign wrapping the $lhs$. Therefore we could have four contact points as possible candidates. The two red lines indicate the maximum and minimum value:
We can take a look at the animation.
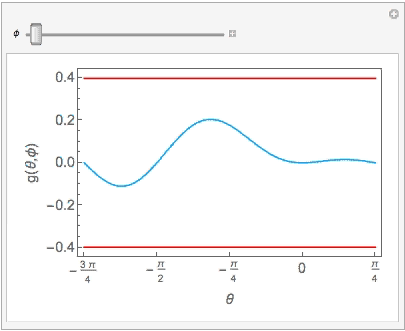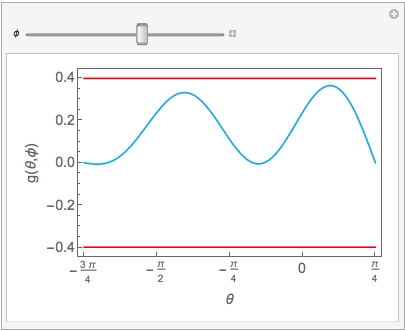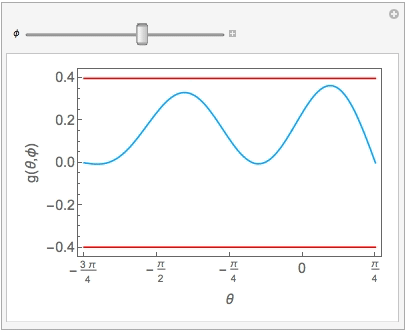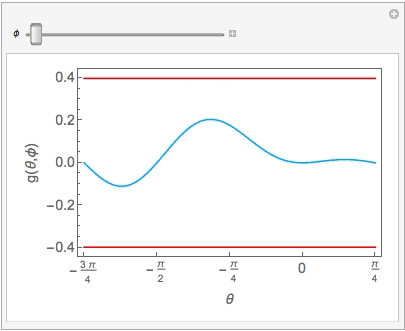
some contact points on the left side during the animation should be disregarded because our region plot shows that these points do not give $a > b > c$. Comparing to the 3D plot for the $g(\theta,\phi)$, we shall discard left half of the curve when $phi$ is greater than $-1$.
Wolfram language's built in function NMaximize (NMinimize) and FindMaximum(FindMinimum) should work both well in this case with slow oscillating funcitons. The only difference is that FindMaximum requires initial guess. With the aid of visualization it wouldn't be challenging. Both method converges fast and gives a result in a fraction of second.
This is some valid solution:
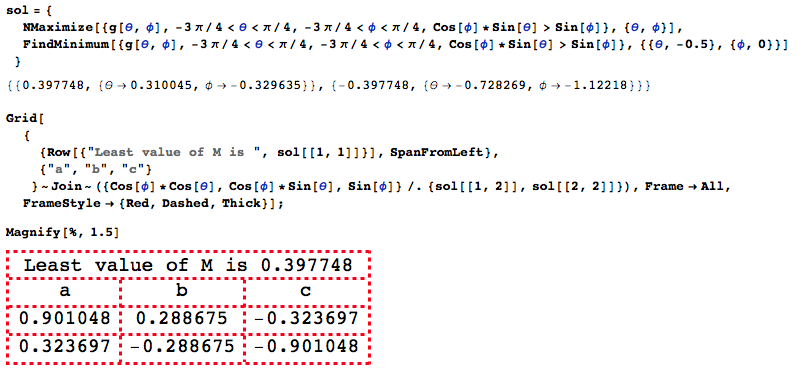
The result I have matches the official solution $M \geq 9/(16\sqrt(2)) = 0.397748 $
Use the link below to download the notebook.
 Attachments:
Attachments: