You have to use patterns: Subscript[A, n_] =, just as in function definitions.

Another thing:

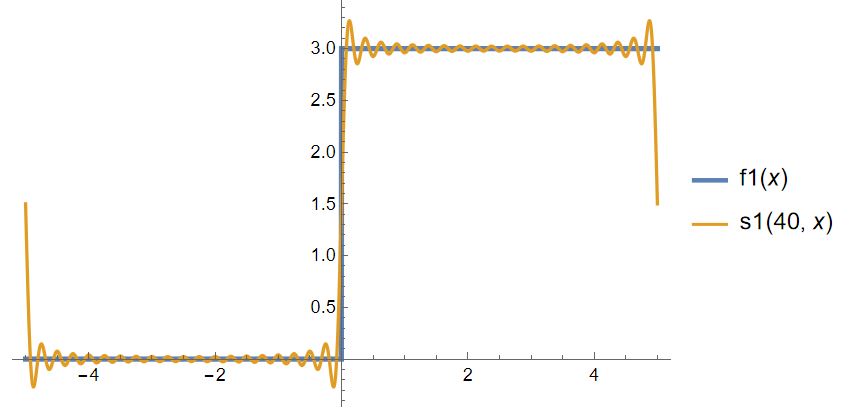
When I use subscripts for 0 and n at A0, An, and Bn then it doesn't calculate... how can I use subscripts at A0, An, and Bn? Is such a thing possible?

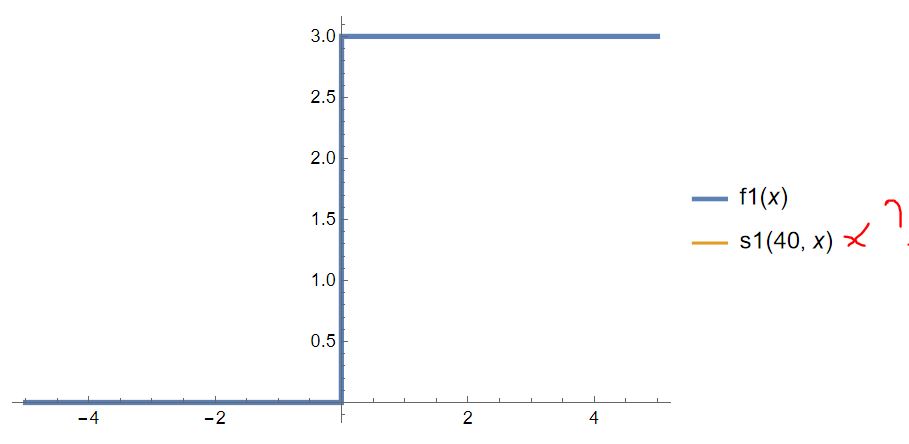
In principle, I think I found out why those sums are not calculated when I use subscripts at those variables. For example:

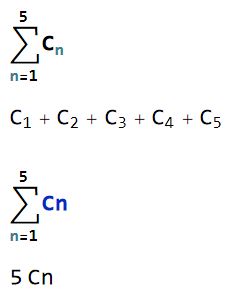
But I'm interested if there is any way to use subscripts for those sums...?

f1[x_] := \!\(\*
TagBox[GridBox[{
{"\[Piecewise]", GridBox[{
{"0", 
RowBox[{
RowBox[{"-", "5"}], "<", "x", "<", "0"}]},
{"3", 
RowBox[{"0", "<", "x", "<", "5"}]}
},
AllowedDimensions->{2, Automatic},
Editable->True,
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.84]}, 
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}},
Selectable->True]}
},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.35]}, 
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}}],
"Piecewise",
DeleteWithContents->True,
Editable->False,
SelectWithContents->True,
Selectable->False,
StripWrapperBoxes->True]\)
Plot[f1[x], {x, -5, 5}, Exclusions -> None]
T = 10;
Subscript[A, 0] = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f1[x] \[DifferentialD]x\)\) // Simplify
Subscript[A, n] = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f1[x]*Cos[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] \[DifferentialD]x\)\) // 
  Simplify
Subscript[B, n] = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f1[x]*Sin[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] \[DifferentialD]x\)\) // 
  Simplify
s1[k_, x_] := Subscript[A, 0]/2 + \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 1\), \(k\)]\((
\*SubscriptBox[\(A\), \(n\)]*Cos[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] + 
\*SubscriptBox[\(B\), \(n\)]*Sin[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]])\)\) // Simplify
Testf1 = 
  FourierSeries[f1[x], x, 40, 
   FourierParameters -> {-(1/5)*\[Pi], 1/5*\[Pi]}];
Plot[{f1[x], s1[40, x]}, {x, -5, 5}, Exclusions -> None, 
 PlotLegends -> "Expressions", 
 PlotStyle -> {Thickness[0.008], Thickness[0.005], Thickness[0.003]}]

Attachments:

Untitled-1.nb

Ok. Thank you.

Testf1 = 
  FourierSeries[f1[x], x, 40, 
   FourierParameters -> {-(1/5)*\[Pi], 1/5*\[Pi]}];