Group Abstract Group Abstract

Message Boards Message Boards

0
|
6.9K Views
|
25 Replies
|
5 Total Likes
View groups...
Share
Share this post:

How can I change values ​​in radians (pi) for x axis on ListPlot?

Cornel B.
Posted 3 years ago

Hello,

ListPlot[Sqrt[A[n]^2 + B[n]^2] /. n -> {1, 2, 3, 4, 5, 6, 7, 8}, 
 PlotRange -> {{0*\[Pi], 2*\[Pi]}, Automatic}, Filling -> Axis]

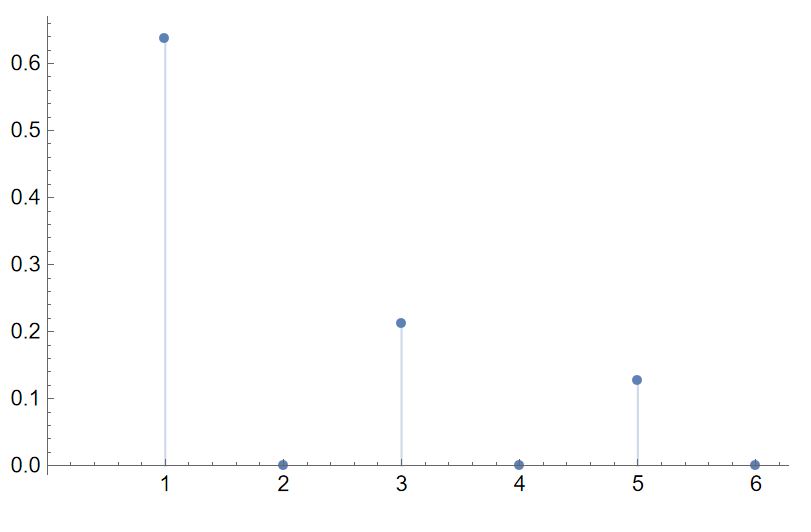
enter image description here

How the x-axis looks now is like when 1 would be pi, 2 would be 2pi, 3 would be 3pi, etc:

enter image description here

ListPlot[Sqrt[A[n]^2 + B[n]^2] /. n -> {1, 2, 3, 4, 5, 6, 7, 8}, 
 PlotRange -> {{0*\[Pi], 3*\[Pi]}, Automatic}, Filling -> Axis, 
 Ticks -> {{0*\[Pi], 1*\[Pi], 2*\[Pi], 3*\[Pi]}, Automatic}]

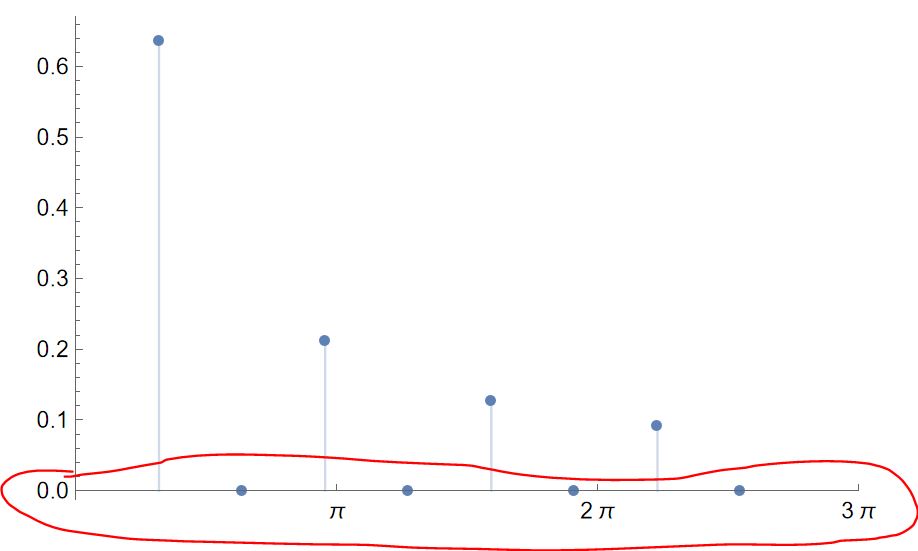
enter image description here

How can I make the x-axis look like this? Is it possible?

enter image description here

Mathematica 13.2 Notebook file attached.

Thank you.

Entire code:

f5[x_] := \!\(\*
TagBox[GridBox[{
{"\[Piecewise]", GridBox[{
{"1", 
RowBox[{"0", "<", "x", "<", "1"}]},
{"0", 
RowBox[{"1", "<", "x", "<", "2"}]}
},
AllowedDimensions->{2, Automatic},
Editable->True,
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.84]}, 
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}},
Selectable->True]}
},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.35]}, 
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}}],
"Piecewise",
DeleteWithContents->True,
Editable->False,
SelectWithContents->True,
Selectable->False,
StripWrapperBoxes->True]\)
Plot[f5[x], {x, 0, 2.5}, Exclusions -> None];
T = 2 - 0;
A0 = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f5[x] \[DifferentialD]x\)\) // Simplify;
A[n_] = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f5[x]*Cos[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] \[DifferentialD]x\)\) // 
   Simplify;
B[n_] = 2/T*\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-
\*FractionBox[\(T\), \(2\)]\), 
FractionBox[\(T\), \(2\)]]\(f5[x]*Sin[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] \[DifferentialD]x\)\) // 
   Simplify;
s5[k_, x_] := A0/2 + \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 1\), \(k\)]\((A[n]*Cos[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]] + B[n]*Sin[
\*FractionBox[\(2*\[Pi]*n*x\), \(T\)]])\)\) // Simplify;
ListPlot[Sqrt[A[n]^2 + B[n]^2] /. n -> {1, 2, 3, 4, 5, 6, 7, 8}, 
 PlotRange -> {{0*\[Pi], 3*\[Pi]}, Automatic}, Filling -> Axis, 
 Ticks -> {{0*\[Pi], 1*\[Pi], 2*\[Pi], 3*\[Pi]}, Automatic}]
Attachments:
Untitled-4.nb
POSTED BY: Cornel B.
25 Replies
Sort By:

Quantity[3, "Degrees"] is replaced internally by Quantity[3, "AngularDegrees"], just the way Quantity[3, "s"] is replaced by Quantity[3, "Seconds"].
POSTED BY: Gianluca Gorni

If you write simply k instead of {k, Quantity[k, "AngularDegrees"]} you get the numbers without the degree marker.
POSTED BY: Gianluca Gorni

The tick specification {a, b} means that in position a we get the tick label b. In the case {Pi,Pi} the effect of is the same as simply Pi, you are right.
POSTED BY: Gianluca Gorni

You want degrees instead of radians on the y axis? Then you have to convert the values:

ListPlot[Table[{n*Pi, Limit[ArcTan[B[k]/A[k]],
     k -> n, Direction -> -1]/Degree}, {n, 1, 8}],
 Filling -> Axis, FillingStyle -> Red,
 Ticks -> {Table[{k Pi, k Pi}, {k, 8}],
   Table[{k, Quantity[k, "AngularDegrees"]},
    {k, -90, 0, 30}]}]
POSTED BY: Gianluca Gorni

Try the option

Ticks -> {{#, # Pi} & /@ Range[8], Automatic}

A simple glance into the documentation would have done it ...
POSTED BY: Henrik Schachner
Cornel B.
Cornel B.
Posted 3 years ago

Gianluca Gorni Thank You anyway for your support in this hole topic (from the begginning)
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

I think that AngularDegrees îs used for Radian repesentation, and Degrees for ° (Degree repesentation)...(but If someone knows better then he/she can tell to us)
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

But even when I put Degrees instead of AngularDegrees little o it still remained (I posted already this above):

enter image description here

It's strange because there are 2 different names that seem to represent the same thing. There should normally be some difference between them (if it exists)...but there might not be any difference as well. The question is only when we know that we have to use AngularDegrees instead of Degrees...
POSTED BY: Cornel B.

I suppose it depends on what you want to get. I suggested "AngularDegrees" because you requested the little o on the y axis. You could achieve that same effect in other ways, presumably. Anyway,

Sin[Quantity[3, "AngularDegrees"]] == Sin[3 Degree]

gives True.
POSTED BY: Gianluca Gorni
Cornel B.
Cornel B.
Posted 3 years ago

And then which one should I use further to represent the degree in calculations and in Ticks, Table, etc: AngularDegrees or Degrees? So as not to expect wrong results or misinterpretations by Mathematica...Which would be the most suitable or better option between the 2? Which option from the 2 would you choose if you had to choose?
POSTED BY: Cornel B.

"AngularDegree" is the official name, and it is a string, not a symbol. Its use is confined to Quantity, UnitConvert and similar functions. If you type Quantity[3,"Degree"], the system automatically replaces "Degree" with "AngularDegree", but you may never realize it, because by default it is displayed as the little o.

Degree is a symbol, not a string. It is replaced by the number Pi/180 when making calculations, like for example GoldenRatio, which is replaced by 1/2 (1 + Sqrt[5]). It is also rendered by the little o.

The output form of 3 Degree looks almost the same as Quantity[3,"Degree"]. I leave it to you to discover the differences.

There is indeed some margin for confusion.
POSTED BY: Gianluca Gorni
Cornel B.
Cornel B.
Posted 3 years ago

I don't know what to say, Degree has an expression (Pi/180, which is ok), and AngularDegree has no expression, although it tells you in the result that Degree would be AngularDegree...

enter image description here

enter image description here
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

So I should rely on AngularDegree when I want to use Degree, right? (Degree = AngularDegree) Although it is strange that we have to write AngularDegree instead of Degree when we refer to Degree, although there are both forms of AngularDegree and Degree available. What will be the difference between them then...? When should we use AngularDegree, and when should we use Degree?

enter image description here
POSTED BY: Cornel B.

It is somewhat confusing.
POSTED BY: Gianluca Gorni

The symbol Degree is much older than the Quantity framework. Degree is a numerical constant, equivalent to Pi/180, the value of a degree in radians. It is not a Quantity.

Degree // FunctionExpand
POSTED BY: Gianluca Gorni

Try this input:

Quantity[3, "Degrees"] // FullForm
POSTED BY: Gianluca Gorni

When I type Quantity[3, "Degree in the FrontEnd, it does not give me the option "Degrees". I suppose it is safer to write "AngularDegrees", as it is less ambiguous, as degrees are used also for temperatures.
POSTED BY: Gianluca Gorni
Cornel B.
Cornel B.
Posted 3 years ago

And regarding the AngularDegree and Degree, what is the difference between these 2? (because the results between them seems to be equal...from what I can see):

enter image description here

Degree is of course Degree, and I think AngularDegree means radian (rad). And if we want Quantity to remain in Degree then we leave {k, -90, 0}, and if we want to put in Qunatity AngularDegree (which is Radian(Rad)) then we should put {k, -90Pi/180, 0Pi/180}, am I interpreting correctly? Do you know?

enter image description here
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

I think that is something based on this:

enter image description here

But I don't yet know how to understand this thing...how does this influence things.
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

Thanks Gianluca Gorni.

I am not sure here for Ticks why we need to put in Table {kPi, kPi} instead of k*Pi, because the results are the same:

enter image description here

enter image description here

Is it necessary to put that {kPi, kPi}? Or is it enough only {k*Pi}?
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

By now, Amplitude vs Radian is ok (both for the x-axis and the y-axis):

enter image description here

But Phase vs Radian is not ok (only for the y-axis):

enter image description here
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

There are two different graphs involved:

enter image description here

enter image description here

You combined both: enter image description here
POSTED BY: Cornel B.
POSTED BY: Gianluca Gorni
Cornel B.
Cornel B.
Posted 3 years ago
Attachments:
Untitled-4.nb
POSTED BY: Cornel B.
Cornel B.
Cornel B.
Posted 3 years ago

Thanks. I did not find such a code for Ticks in the documentation. Or what kind of documentation do you look at?

https://reference.wolfram.com/language/

https://reference.wolfram.com/language/ref/Ticks.html

I think that here it is more about the experience than documentation...

I do not understand this: 

{#, # Pi} & /@ Range[8]

I understand Range[8] and how it relates to my code, but that {#, #Pi} and &/@ not yet :

enter image description here

enter image description here
POSTED BY: Cornel B.
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard