I'm not a expert for solving this kind equation, but using FiniteElement method with coefficient = 3/2, I have:

     usol2 = Block[{\[Epsilon] = $MachineEpsilon, inf = 48, 
         coeff = 1 + 1/2}, 
        NDSolveValue[{I*
            D[M[r, t], 
             t] == (-E^-M[r, t])*(D[M[r, t], r, r] - (D[M[r, t], r])^2 + (
               2 D[M[r, t], r])/r) - 
            NeumannValue[M[r, t], r == \[Epsilon]], 
          DirichletCondition[M[r, t] == coeff*E^(-(r^2/2)), t == 0], 
          DirichletCondition[M[r, t] == 0, r == inf]}, 
         M, {r, \[Epsilon], inf}, {t, 0, 2}, 
         Method -> {"FiniteElement", "InterpolationOrder" -> {M -> 2}, 
           "MeshOptions" -> {"MaxCellMeasure" -> 2/100}}]];
     xv = NArgMax[Norm[usol2[0, t]], {t, 1/10, 5/10}];
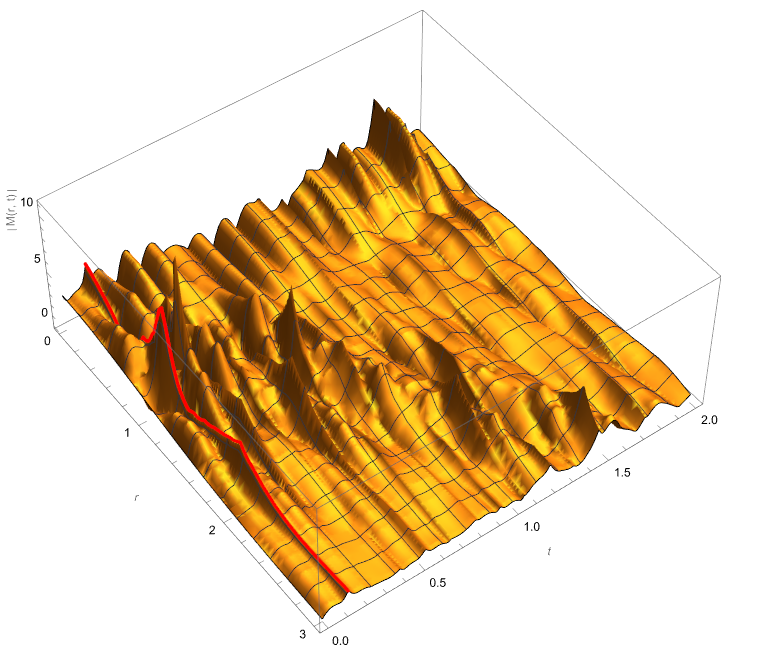
     Show[Plot3D[2 Norm[usol2[r, t]], {r, 0, 3}, {t, 0, 2}, 
       PlotRange -> All, 
       AxesLabel -> {Style["r ", Italic], Style["t", Italic], 
         Rotate["\[LeftBracketingBar]M(r, t)\[RightBracketingBar]", \[Pi]/
          2]}, ViewPoint -> {3, -2.2, 4.1}, MaxRecursion -> 4], 
      ParametricPlot3D[{r, xv, 2 Norm[usol2[r, xv]]}, {r, 0, 3}, 
       PlotStyle -> Directive[Red, Thickness -> 0.005]]]

Maybe you post question here ,you got a better answer.

Regards M.I.

Hi @Tao, are you looking for numeric or exact symbolic solution? If numeric, would solutions for large enough (but not infinity) radius suffice as an approximation? If you have any other thoughts or background or references for this problem, it would be very helpful, as well as any initial setup in form of Wolfram Language code that you have may tried already.