I'm not a expert for solving this kind equation, but using FiniteElement method with coefficient = 3/2, I have:
usol2 = Block[{\[Epsilon] = $MachineEpsilon, inf = 48,
coeff = 1 + 1/2},
NDSolveValue[{I*
D[M[r, t],
t] == (-E^-M[r, t])*(D[M[r, t], r, r] - (D[M[r, t], r])^2 + (
2 D[M[r, t], r])/r) -
NeumannValue[M[r, t], r == \[Epsilon]],
DirichletCondition[M[r, t] == coeff*E^(-(r^2/2)), t == 0],
DirichletCondition[M[r, t] == 0, r == inf]},
M, {r, \[Epsilon], inf}, {t, 0, 2},
Method -> {"FiniteElement", "InterpolationOrder" -> {M -> 2},
"MeshOptions" -> {"MaxCellMeasure" -> 2/100}}]];
xv = NArgMax[Norm[usol2[0, t]], {t, 1/10, 5/10}];
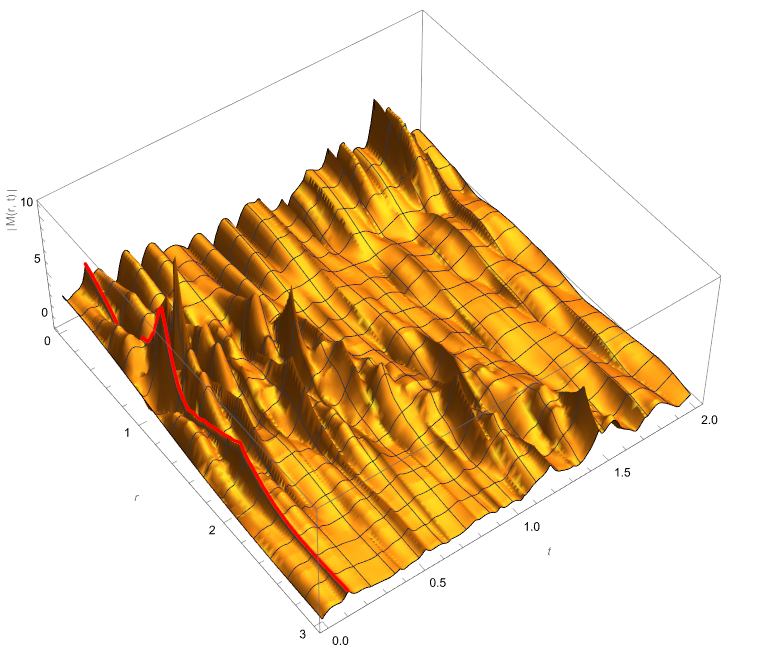
Show[Plot3D[2 Norm[usol2[r, t]], {r, 0, 3}, {t, 0, 2},
PlotRange -> All,
AxesLabel -> {Style["r ", Italic], Style["t", Italic],
Rotate["\[LeftBracketingBar]M(r, t)\[RightBracketingBar]", \[Pi]/
2]}, ViewPoint -> {3, -2.2, 4.1}, MaxRecursion -> 4],
ParametricPlot3D[{r, xv, 2 Norm[usol2[r, xv]]}, {r, 0, 3},
PlotStyle -> Directive[Red, Thickness -> 0.005]]]
Maybe you post question here ,you got a better answer.
Regards M.I.