It is wired because for what I saw until now it is not possible to do unwrapping of phase of bode plot inside the BodePlot[...] command in a more simple manner in Mathematica, and only way is to extract the points from the PhasePlot of BodePlot and then doing something like Henrik did, which is something not so straight forward, mainly if someone is a beginner. And we are talking here that this unwrapping of phase plot of bode plot is something that someone who deals with control systems and signal processing will encounter very often, therefore unwrapping of phase of bode plot I think it should have already taken into account and have been implemented by the developers of wolfram mathematica...

Cornel,

I have no experience with BodePlot[] whatsoever and so I do not know whether this unwrapping makes sense in this case. But anyway - here is a simple approach:

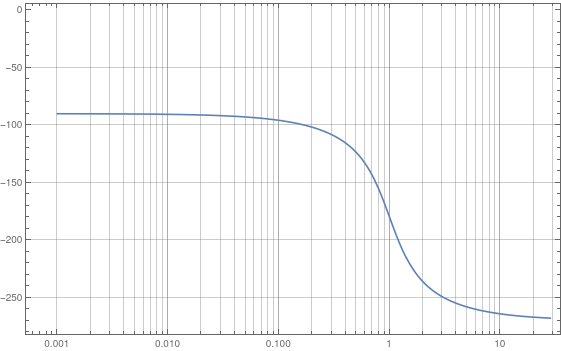
bpl = BodePlot[test, GridLines -> Automatic, PlotRange -> {Automatic, {-270, 0}}, PlotLayout -> "Phase"];
(* extracting point values from the plot: *)
pts0 = First@Cases[bpl, Line[pts__] :> pts, All];
(* "true" x-value: *)
pts = {10^#1, #2} & @@@ pts0;
{{xmin, xmax}, {ymin, ymax}} = MinMax /@ ({xVals, yVals} = Transpose[pts]);
xGrid = Flatten[Range[10] # & /@ PowerRange[xmin, xmax]];

For the unwrapping there is an elegant algorithm from @Peter Karpov in this discussion:

unWrap[\[Tau]_][a_] := a - \[Tau] Prepend[Accumulate[Round[Differences[a]/\[Tau]]], 0]

So - we get:

(* unwrapped result: *)
ptsUnWrapped = Transpose[{xVals, unWrap[ymax - ymin][yVals]}];
ListLinePlot[ptsUnWrapped, ScalingFunctions -> {"Log", None}, GridLines -> {xGrid, Automatic}, Frame -> True]

Does that help? Regards -- Henrik

Other sugestions? So, i want to be able to change the Phase Plot of Bode Plot in following manner from (0, 360) degrees, (90, 450) degrees, (180, 540) degrees, and so on, i think that it is the idea (or at least something like that)

The documentation you're showing is a very old package.

Yes, it looks like older documentation, but that's all I found when I searched for UnwrapPhase for Bode Plot...

I'll also look at PhaseRange (I tried now quickly by putting PhaseRange -> {-Pi, Pi} (but also other combinations), but it didn't work for me so far...I didn't manage to find the right combination until now. If anyone has found a solution then it is welcome.