Vertex configuration (3,11,11) can grow forced to 1-super-tile, which is like a "seed".

(The yellow tiles are new, unreflected and brown tiles are new, reflected.)

And this vertex configuration shows up as the green vertex in the TrialityTree, always as an end leaf:

What's more, it means that each vertex configuration 3,11,11 determines a 1-super-tile. So, in the cluster, it is not only "leaf" that simple, it is unique in the corresponding 1-super-tile. In the 2-super-tile, there are 7 such configurations and each one corresponds to a 1-super-tile:

(PS: It is titled as (4,12,12), which is same as (3,11,11) configuration. Just different index offset.)

In the figure above, the yellow hats are reflected and blue are unreflected. The darker colored 3-hats combinatorics is 3,11,11, and the white points are where they meet.

Additionally, the rotation angle of the (3,11,11) configuration consists with that of 1-super-tile preciously. The position of (3,11,11) in its 1-super-tile is fixed.

By the way, there are no any other vertex configurations with this property.

In other words, as soon as a (3,11,11) appears, we can immediately know how to extend it to a 1-super-tile.

Maybe it will be useful to construct the cluster?

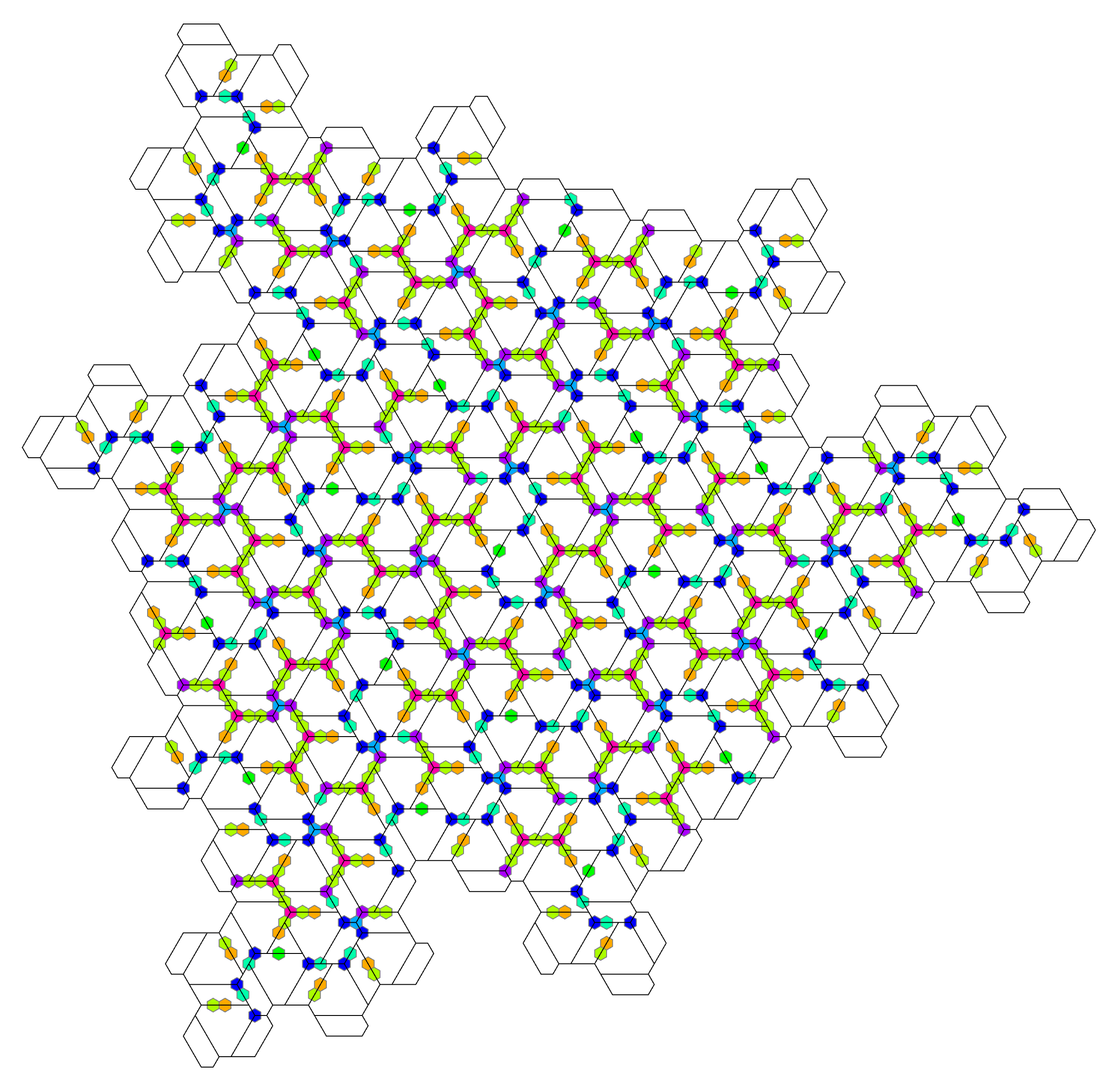
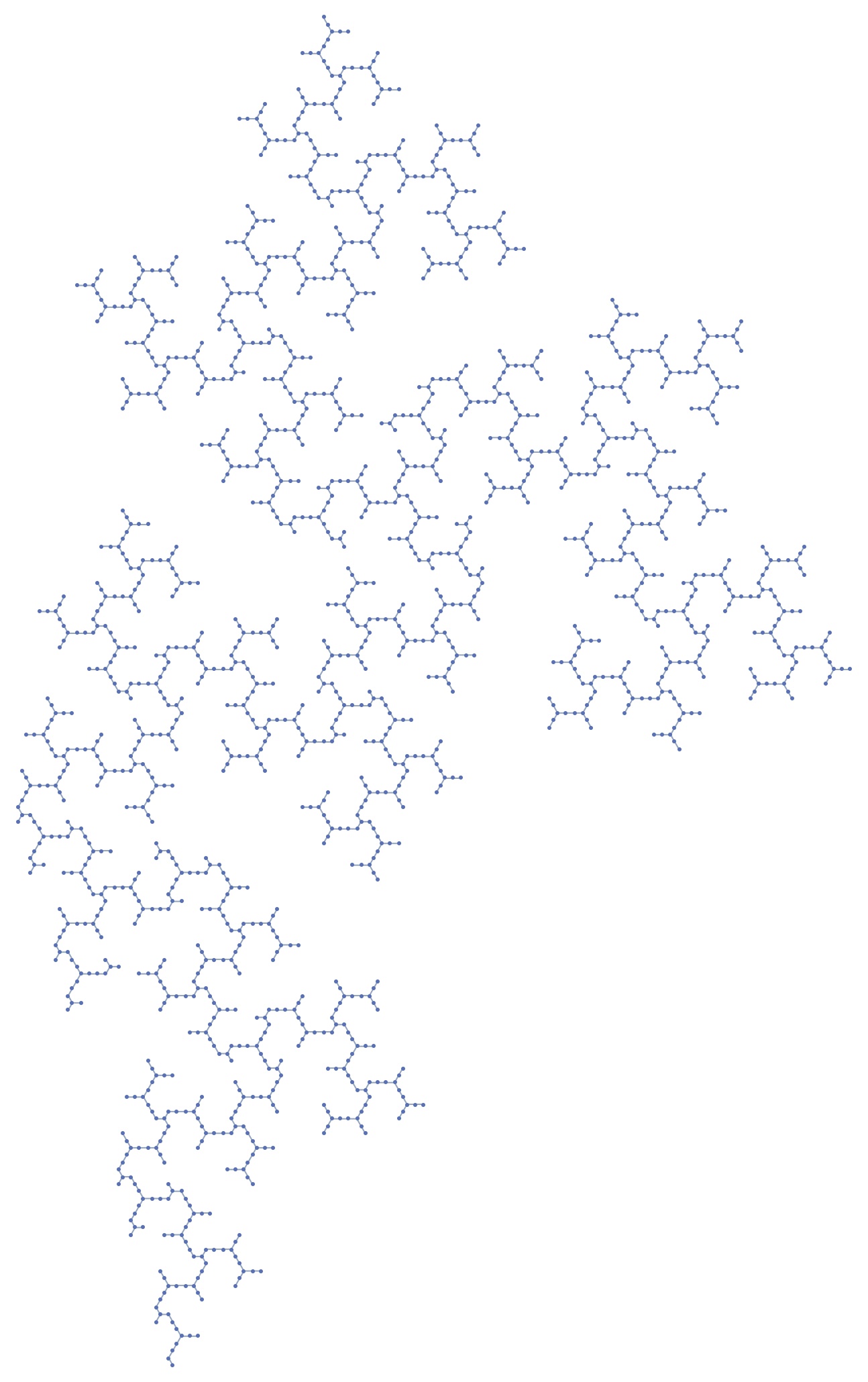
After a few hours computing overnight, we now have two more terms by brute force:

1, 2, 9, 13, 53, 72, 295, 392, 1623

And it's very likely these numbers are determined by the following conjectural function:

TrialityTreeVertexCount[ind_] := Module[{inf, infm},
  inf = {
    1 -> {1, 1, 2, 2, 2, 8},
    2 -> {1, 2, 2, 2, 2, 8},
    3 -> {1, 1, 2, 2, 2, 2, 4, 7, 8},
    4 -> {1, 2, 2, 2, 2, 2, 4, 7, 8},
    5 -> {2, 2, 2, 2, 2, 2, 8},
    6 -> {5, 6, 6, 7},
    7 -> {5, 6, 7, 7},
    8 -> {5, 7, 7, 7}
    };
  infm = Outer[Count[#2, #1] &, Range[8], inf[[All, 2]], 1];
  Riffle[
   Total /@ NestList[Dot[infm, #] &, {0, 0, 1, 0, 0, 0, 0, 0}, ind],
   Total /@ NestList[Dot[infm, #] &, {0, 0, 0, 1, 0, 1, 0, 0}, ind]
   ]
  ]

TrialityTreeVertexCount[10]

Out[] = {1, 2, 9, 13, 53, 72, 295, 392, 1623, 2137, 8903, 11676, 
48793, 63878, 267321, 349693, 1464365, 1914924, 8021215, 10487564, 
43935927, 57441265}

Oh, I missed that you used Eisenstein on the einstein. Could the EisensteinInteger WFR function help at all?

Hi Paul and Ed,

When I say "Eisenstein Integers" I just mean hexagonal lattice + group action. Divisibility properties are not necessary in any of my calculations so far. It's possible that Eisenstein integers have some interesting relative structure, but it's unlikely to be more than just a curiosity. The reason is that the tiling (or one of its MLD color patterns) is a Delone set, while Eisenstein primes are known not to be a Delone set. Thus it would be kind of an "apples to oranges" comparison, but you might be able to get some trivia out of it.

In more recent calculations I've done, I actually used complex numbers in the data model. Unfortunately, the calculation design was constrained by my own ignorance, and didn't even bother to limit the number of complex multiplications + expand. It turned out slow, but the results are still amazing:

I'm giving away too many of my secrets here, but the reason is that they don't make good secrets anyways. If we keep following leads from the color patterns, I think we're going to get a more intuitive proof of the tiling and all its properties sooner rather than later (and in WL). Students might be interested to participate during summer school. It would be a great exciting project, with no relation to LLM's whatsoever.

Theorem (tentative). The triality pattern on the hexagonal lattice is MLD to the Hat tiling.

Sketch of Proof:

Define missing centers parity pattern on the hexagonal lattice to have value Red if the vertex falls inside a hat, and value Blue if it falls on an edge. The alignment is such that the edges around coincident hat vertices open at an angle either 2Pi/3 or 4Pi/3 (as in Fig. 1.1).

Every vertex is also touched by one, two or three hat tiles. This allows a three coloring, the triality pattern. The parity pattern is a factor of the triality pattern, which merges the sets of vertices touching either two or three hats (dark green and light blue).

[ Depicted in previous post ]

Every edge in the HFTP tiling goes back to at least one Trigonal-symmetric Y-join.

In the parity pattern, the three joins are centered on a blue tile surrounded by three red tiles at equal angles. The edges extend through blue tiles until before they hit a red tile (sometimes making a Y-T-edge, sometimes a Y-Y-edge).

This accounts for all the edges of the PTHF tiling, but not necessarily for the A/B edge type parity split. (?)

The A/B parity split is determined by splitting the blue parity symbol into light blue and dark green triality symbols.

[ Edit: This is only usually true: B edges are GBBBG, A edges are BBGGG. ]

It will take some more work, but looking at overlays, it seems almost obviously true.

I don't know, someone probably does, if the A/B parity split can be derived only from the parity pattern / FHPT edges pattern, then a stronger theorem would be possible.

Very nice! I decided to take a look at the component hexagons. They are either part of a Y division of a hexagon, or an upside down-Y division of a hexagon. So we can color each hexagon.

Alternately, we can just color the triples.