Hello, All! Back in 2011 The Mathematica Journal published this article I wrote: https://www.mathematica-journal.com/2011/05/11/indexing-strings-and-rulesets/
I needed to refer to Cantor's idea for enumerating the rational numbers by taking diagonal stripes through a doubly infinite table listing all fractions with all positive integer numerators and denominators, and rather than finding an image somewhere I wrote some code to generate the image as a Graph object.
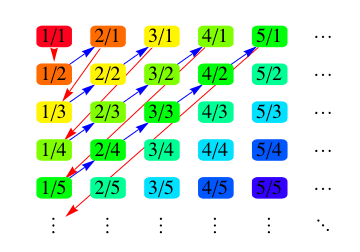
Here's the code, which actually still runs under Mathematica 13.1, but with deprecated Options showing in red all over the place:
Successor[{n_Integer, d_Integer}] := If[d == 1, {1, (n + 1)}, {(n + 1), (d - 1)}];
display[{n_, d_}] := Style[Which[n == d == 6, "\[DescendingEllipsis]", n == 6,
"\[CenterEllipsis]", d == 6, "\[VerticalEllipsis]", True, ToString@Row[{n, d}, "/"]], 20];
GraphPlot[(DeleteCases[#1, Null] &)[Flatten[
Table[{{n, d} -> {n, d}, If[(n <= 7 && d <= 7 && n + d <= 6 && n < 6), {n, d} ->
Successor[{n, d}]]}, {d, 1, 6}, {n, 1, 6}], 3]],
DirectedEdges -> True, VertexLabeling -> True, SelfLoopStyle -> False,
VertexCoordinateRules -> Flatten[Table[{n, d} -> {n, 6 - d}, {d, 1, 6}, {n, 1, 6}], 1],
VertexRenderingFunction -> (If[#2[[1]] < 6 && #2[[2]] < 6,
{EdgeForm[None], Hue[.8 + .09 Plus @@ #2],
Rectangle[#1 - {0.33, .26}, #1 + {0.33, .31},
RoundingRadius -> .11], Black, Text[display@#2, #1]}, Text[display@#2, #1]] &),
EdgeRenderingFunction -> ({If[#2[[1]][[2]] == 1, Red, Blue],
Arrow[#1, If[#2[[1]][[1]] == #2[[2]][[1]] == 1, 0.35, .33]]} &),
AspectRatio -> .7]
Many of these Options for GraphPlot have been replaced by other and more powerful options for Graph. I know I just need to pore over and absorb all the online help examples for Graph, but if anyone here has the time and skills to "translate" this code into Mathematica v.13, I would really appreciate it!
Needed:
(1) Place the vertices as specified, {n,d} is placed in the nth column, dth row.
(2) Format vertices to display {n,d} as n/d in a RoundedRectangle, with fill color assigned by Hue varying as we traverse the enumeration.
(3) Two different edge forms: Blue Arrows for the diagonal steps up and to the right, Red ones (or now I'd probably use a dotted line or arrow) for the retraces connecting one stripe to the next.
Anyone interested / challenged? Many thanks!
Ken