Here is a start
In[1]:= points = {{9, 1}, {9, 1}, {7, 2}, {8, 2}, {7, 3}, {7, 3}, {7,
4}, {8, 4}, {9, 5}, {6, 5}, {6, 6}, {5, 3}, {5, 6}, {5, 6}, {6,
7}, {5, 7}, {5, 7}, {5, 8}, {4, 2}, {4, 4}, {4, 5}, {4, 8}, {3,
6}, {3, 7}, {3, 8}, {3, 8}};
In[2]:= pointLists = GatherBy[pts, Last]
Out[2]= {{{9, 1}, {9, 1}}, {{7, 2}, {8, 2}, {4, 2}}, {{7, 3}, {7,
3}, {5, 3}}, {{7, 4}, {8, 4}, {4, 4}}, {{9, 5}, {6, 5}, {4,
5}}, {{6, 6}, {5, 6}, {5, 6}, {3, 6}}, {{6, 7}, {5, 7}, {5, 7}, {3,
7}}, {{5, 8}, {4, 8}, {3, 8}, {3, 8}}}
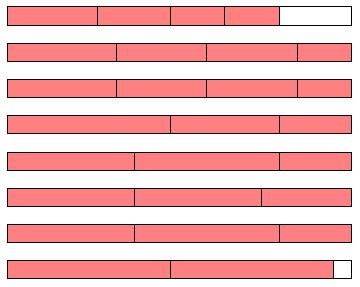
In[3]:= Graphics[
MapIndexed[{EdgeForm[Black], White,
Rectangle[{0, 2 First[#2]}, {19, 2 First[#2] + 1}], Pink,
Function[z,
Rectangle[{z[[1]], 2 First[#2]}, {z[[2]], 2 First[#2] + 1}]] /@
Partition[Join[{0}, Accumulate[#1[[All, 1]]]], 2, 1]} &,
pointLists
]
]
Which gives this picture
Adding the labels and so on would take a bit more work.... ;-)
So, how did I get to this pice of code (which I admit is a bit unreadable...). I solved individual component problems one by one and tested them as I went along. Then as each seemed to work, I incorporated them into the function that I was building up. To make the code clearer, I could break it up into individual pieces which each individually do part of the computation and then put them all into a Module with appropriately named local variables. But to paraphrase Fermat: I do not have time to write it all in the margin. My apologies! I have a busy week but was caught by the challenge of your problem!