You can use NDSolve like this
ode = y'[x] == Cos[x] - Exp[-y[x]];
ic = y[1] == 0;
sol = First[y /. NDSolve[{ode, ic}, y, {x, 0, 2}]]
Plot[sol[x], {x, 0, 2}]
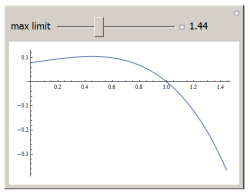
To see what happens as the range changes:
Manipulate[
Module[{sol},
sol = First[y /. NDSolve[{ode, ic}, y, {x, 0, max}]];
Plot[sol[x], {x, 0, max}]
],
{{max, 2, "max limit"}, .1, 4, .01, Appearance -> "Labeled"},
Initialization :>
(
ode = y'[x] == Cos[x] - Exp[-y[x]];
ic = y[1] == 0
)
]
You'll see the singularity after 2.0 show up.