Hi All,
I have a complex function with two independent variables, but aren't easily separated in my function. One is a Laplace variable and the other is a Fourier variable and I would like to bring both back to their respective real spaces and must do so numerically as the function is too convoluted to do symbolically.
I believe I have the right structure, but as it is throwing up a million errors, I wanted to see if anyone had any helpful advice. I have tried looking at other discussions, but I didn't see one that quite fit this niche.
Mathematically, what I am trying to do is: 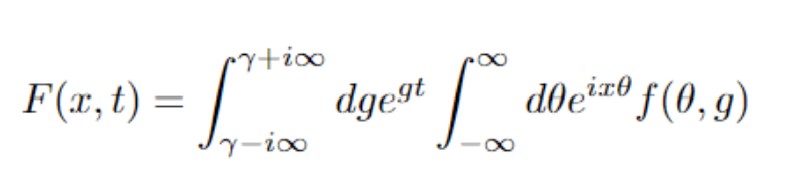
And using the following resources: NInverseLaplaceTransform,NInverseFourierTransform
Needs["FourierSeries`"]
f[g_,s_,\[Omega]0_,k0_,\[Theta]_] := -I 1/\[Pi] g^2/(g^2+\[Omega]0^2) 1/Sinh[k0] Exp[-(g/Abs[k0])Abs[\[Theta]]]/\[Theta];(* Sin[k0 y] *)
tval = 23;
FList:={}
For[i=1,i<=1,i++,xpos = i*0.2;
datap := ResourceFunction["NInverseLaplaceTransform"]
[Simplify[NInverseFourierTransform[f[g,10000,0.5,1,\[Theta]] ,\[Theta],xpos,FourierParameters->{-1,-1}]],g,tval];
AppendTo[FList,datap];
]
Print["Done."]
The f I provide here is one that can be done symbolically, I wanted to use it as a test case but errors abound. I have chosen to loop over only one nonzero x value and one t value as a start.
My understanding of the issue is that the fourier transform will not converge to a value, but will retain itself as a function of g. Then the laplace transform will take care of g.
I hope it is clear what I have presented.
Thanks, Daniel