There are currently 422 dissections at the Wolfram Demonstrations site, so I thought I'd give a talk about them. Here are the records as they stand at Gavin Theobald's Polygon Dissections.
I was also recently intrigued by Quanta's Animation for a six fractal piece square to circle dissection by Andras Máthé, Oleg Pikhurko and Jonathan Noel. 
The following code shows two polygons with the same unit area.
UnitAreaPolyPoints[k_, angle_ : 0] :=
CirclePoints[{Sqrt[2] Sqrt[Csc[(2 \[Pi])/k]/k], angle }, k];
Manipulate[Graphics[{
Line[Append[#, First[#]] &@UnitAreaPolyPoints[j, anglej]],
Line[Append[#, First[#]] &@UnitAreaPolyPoints[k, anglek]]}],
{{j, 3}, 3, 12, 1}, {{k, 5}, 3, 12, 1},
{{anglej, 0}, -Pi, Pi}, {{anglek, 0}, -Pi, Pi},
SaveDefinitions -> True, SynchronousInitialization -> False]
With this, it's possible to prove that a triangle to square dissection requires at least 3 pieces.
New we can start showing dissections. Triangle to Square.
ResourceFunction["CreditedDemonstration"]["EquilateralTriangleToSquare"]
ResourceFunction["CreditedDemonstration"]["HaberdashersProblem"]
ResourceFunction["CreditedDemonstration"]["AnExampleOfTheBolyaiGerwienTheorem"]
ResourceFunction["CreditedDemonstration"]["DissectionOfASphericalTriangleIntoASquare"]
Triangle to Pentagon ResourceFunction["CreditedDemonstration"]["GoldbergsPentagonToTriangleDissection"] We can also get close, as in Pentagon-to-Near-Equilateral-Triangle Dissection.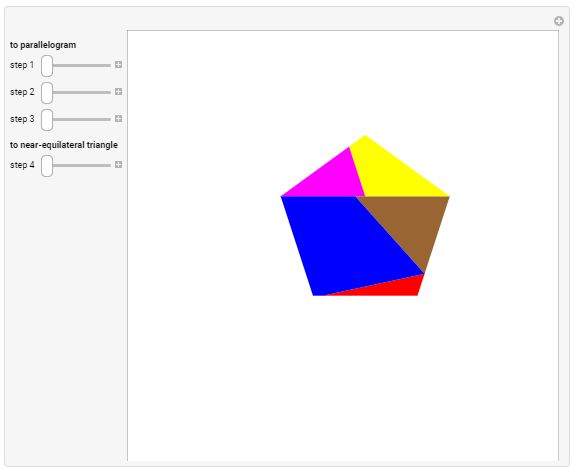 
Triangle to Hexagon ResourceFunction["CreditedDemonstration"]["LindgrensHexagonToTriangleDissection"]
Triangle to Heptagon Theobald's Dissection of a Heptagon to a Triangle
Triangle to Octagon Theobald's Dissection of an Octagon into a Triangle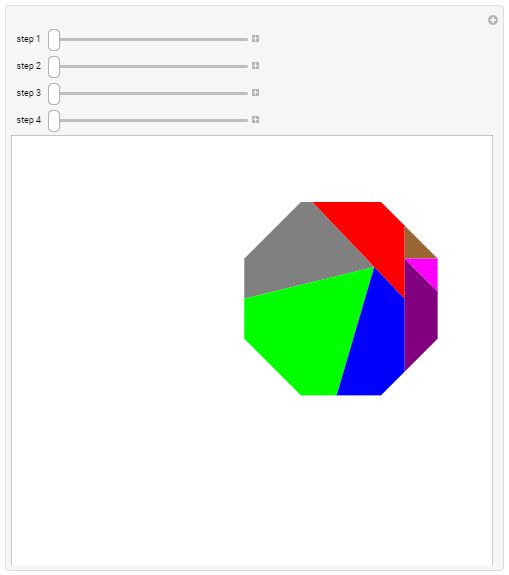 
Triangle to Nonagon Theobald's Nonagon-to-Triangle Dissection and Hanegraaf's Dissection of a Nonagon into a Triangle.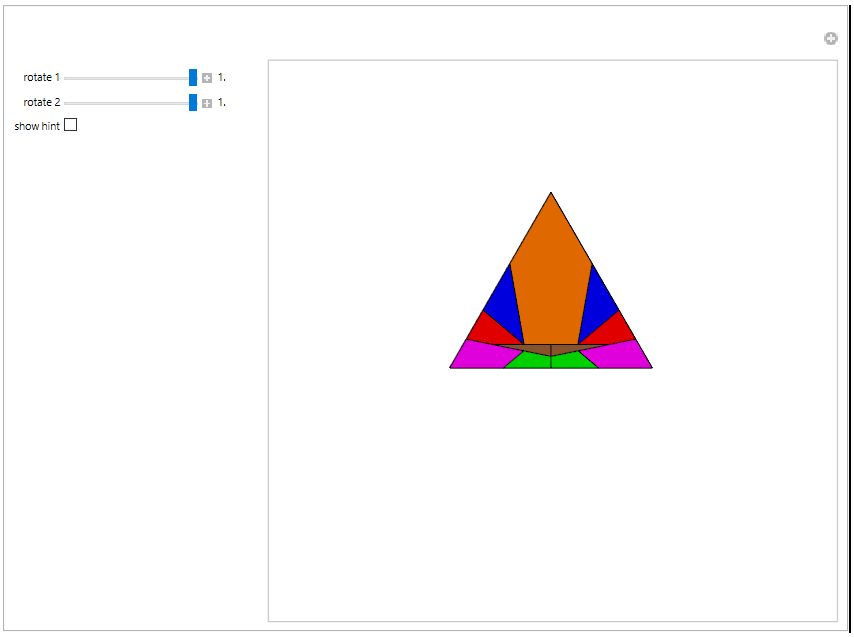 
All of these can be laser cut or 3D printed, as shown by Izidor Hafner. 
Square to Pentagon Freese's Dissection of a Regular Pentagon to a Square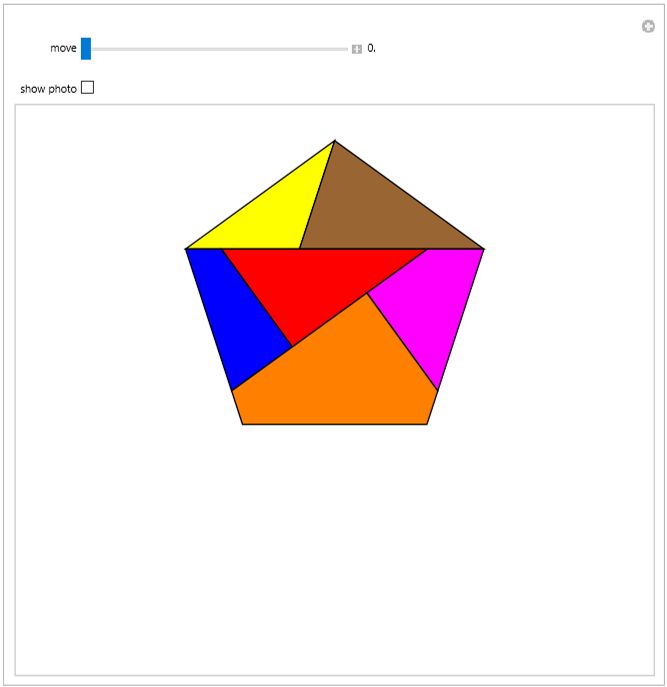 
ResourceFunction["CreditedDemonstration"]["BrodiesPentagonToSquareDissection"]
ResourceFunction["CreditedDemonstration"]["PentagonToNearSquareDissection"]
Adam Gsellman: Pentagon to rectangle is 4.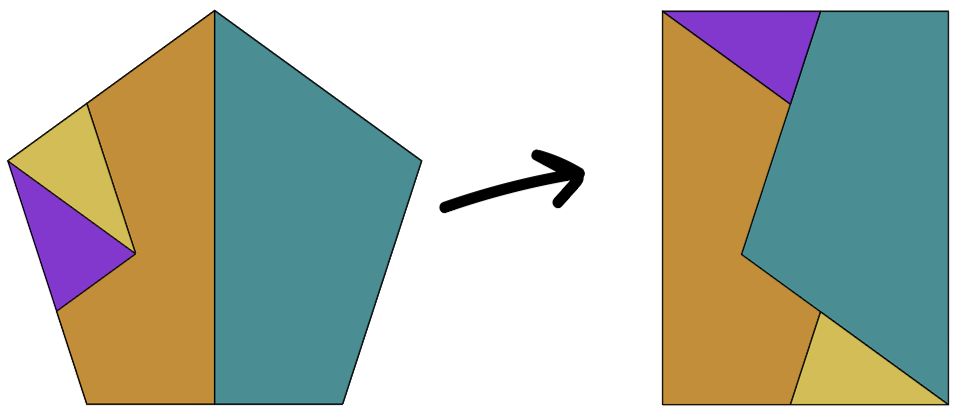 
Square to Hexagon Busschop's Hexagon-to-Square Dissection
ResourceFunction["CreditedDemonstration"]["BradleysHexagramToSquareDissection"]
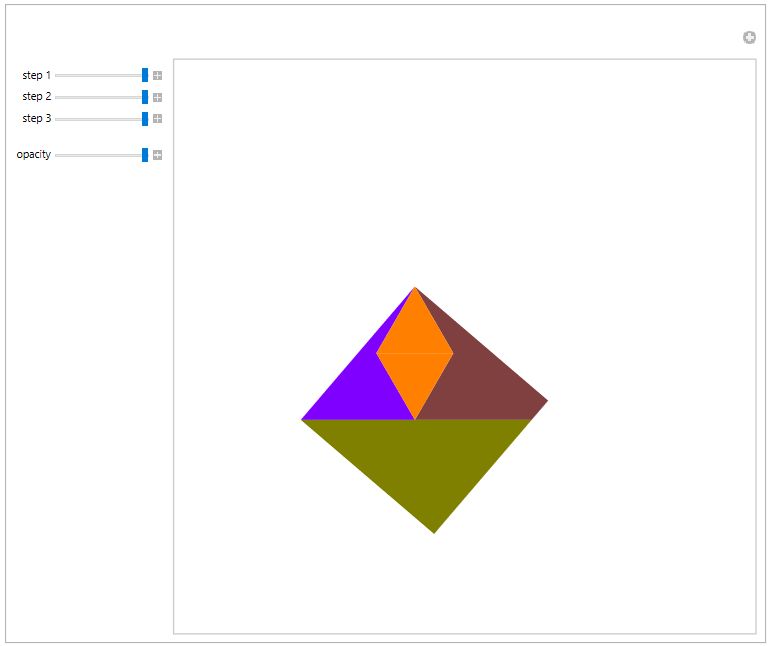
Square to Heptagon Theobald's Heptagon-to-Square Dissection 
Square to Octagon Bennett's Octagon-to-Square Dissection 
Square to Nonagon Theobald's Nonagon-to-Square Dissection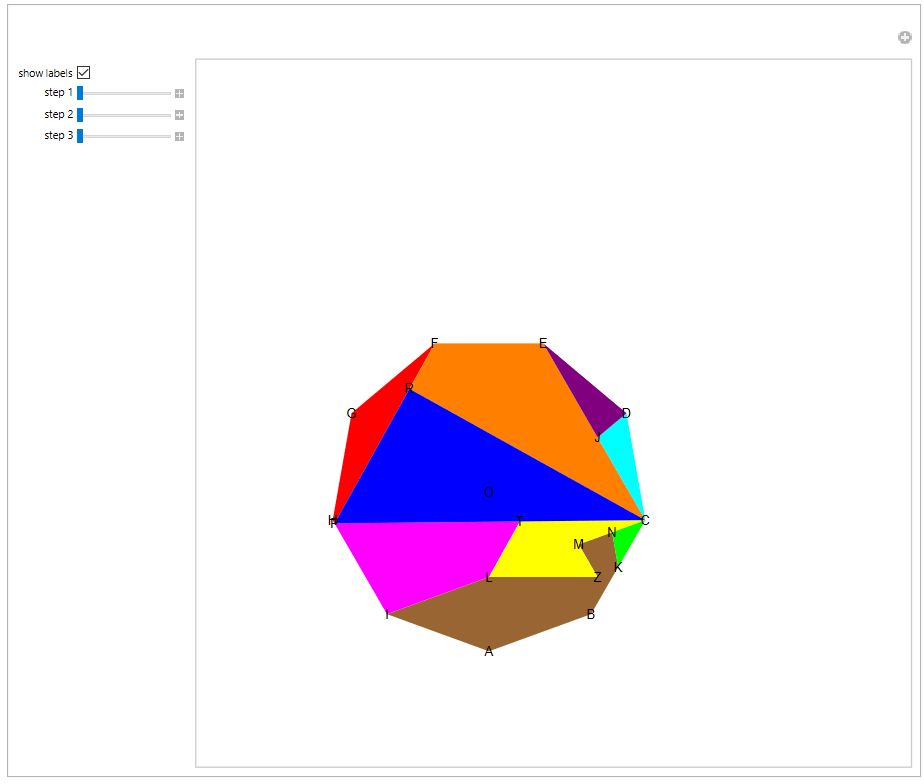 
Square to Decagon Decagon-to-Square Dissection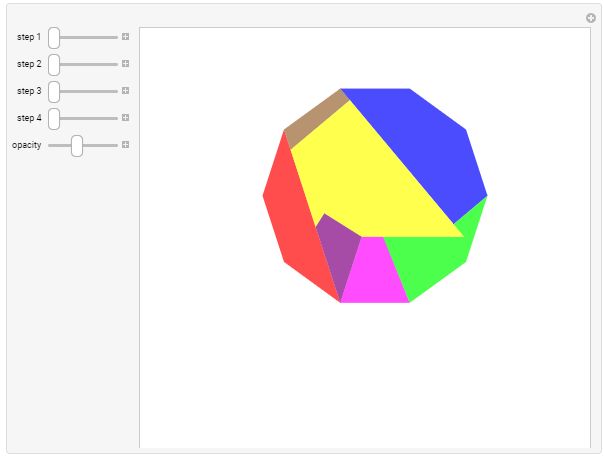 
Square to Dodecagon Freese's Dissection of a Regular Dodecagon into a Square Lindgren's Square-to-Dodecagon Dissection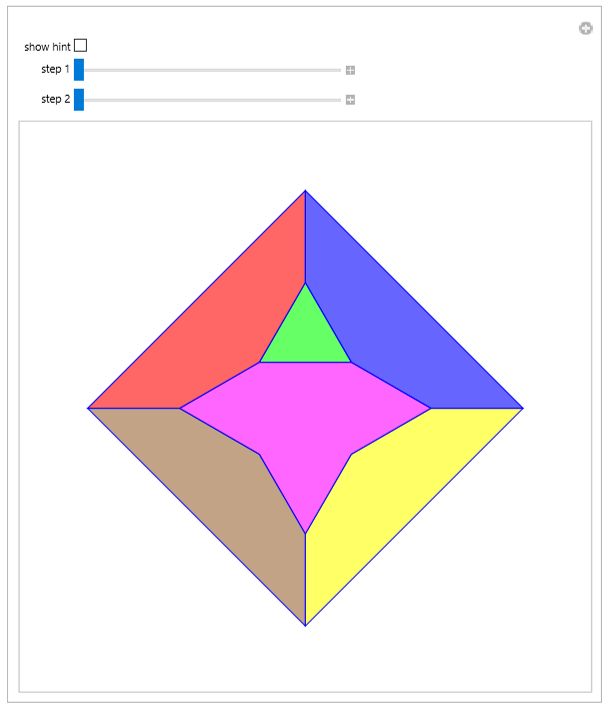 
Pentagon to Hexagon Lindgren's Dissection of a Pentagon to a Hexagon
Pentagon to Heptagon Theobald's Dissection of a Heptagon to a Pentagon
Hexagon to Heptagon Theobald's Heptagon-to-Hexagon Dissection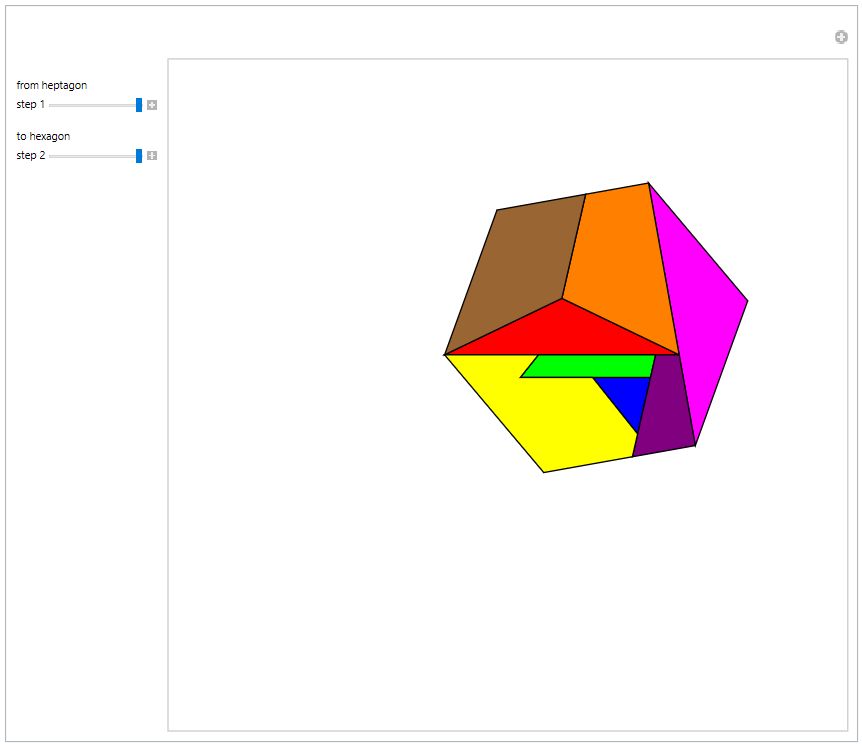 
Hexagon to Dodecagon Dodecagon-to-Hexagon Dissection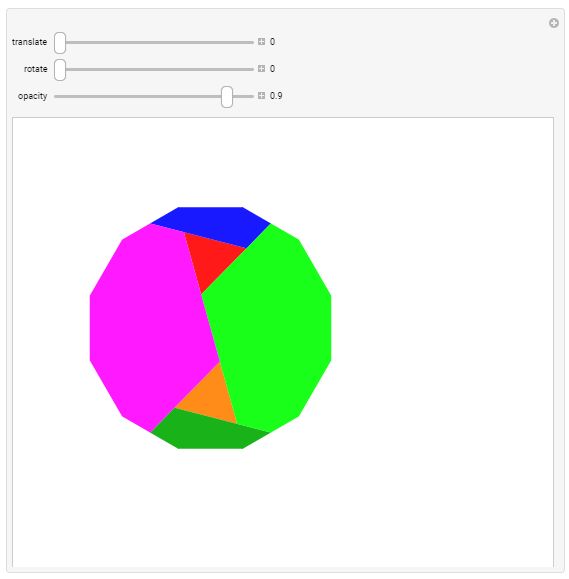 
That shows quite a few ways of transforming one polygon into another. It's also possible to take multiple copies of a polygon and make a larger version of the same polygon.
ResourceFunction["CreditedDemonstration"]["DissectionOfOneRegularHeptagonIntoSeven"]
ResourceFunction["CreditedDemonstration"]["DissectionOfARegularHeptagonIntoEight"]
ResourceFunction["CreditedDemonstration"]["DissectionOfARegularDodecagonIntoThree"]
ResourceFunction["CreditedDemonstration"]["DissectionOfARegularDodecagonIntoSixSmallerOnes"]
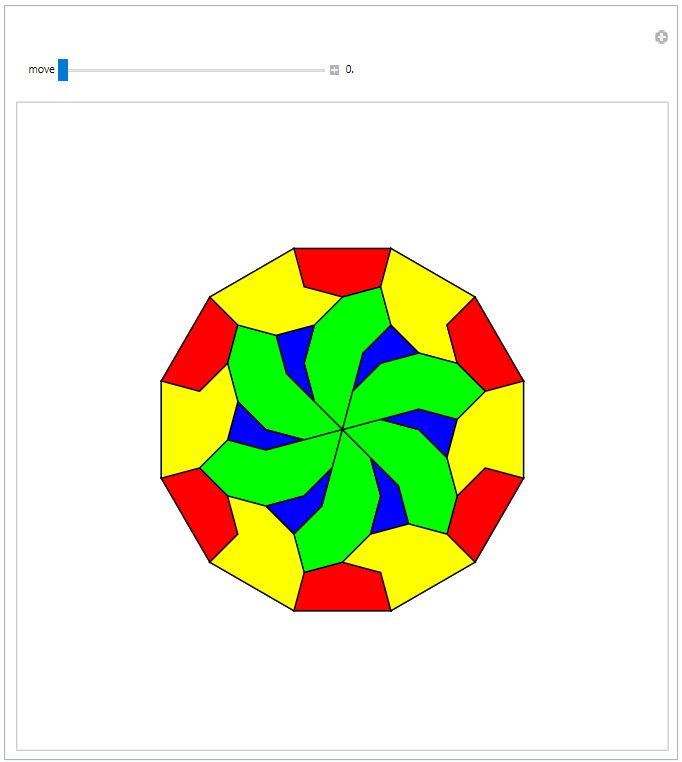
Regular polygons with an edge length of 2 have some odd properties.
1. What is the area of the annulus?
2. What is the square distance sum between vertex heights?
The results of Shattering the Plane came out of a simple question: how can similar triangles surround a point? So far, this question hasn't been answered in 3D with tetrahedra.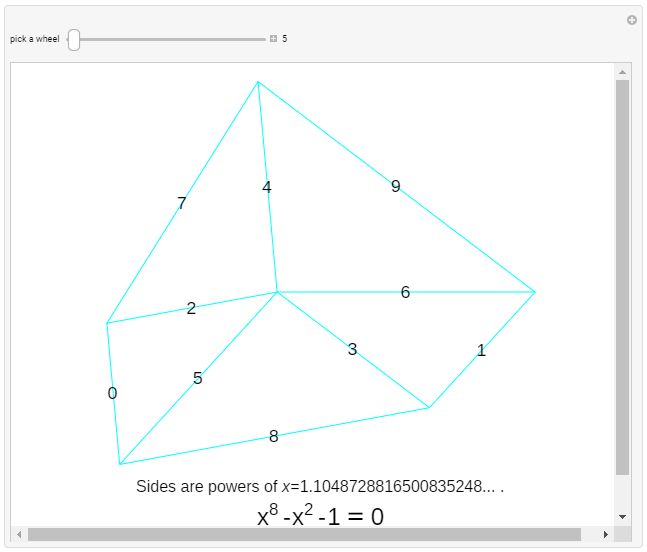 
That particular dissection leads to the following substitution tiling: 
Wallace[Dash]Bolyai[Dash]Gerwien theorem: Two polygons of the same area can be dissected into each other. Discovered independently by Wallace: 1807, Bolyai: 1833, Gerwein: 1835. Hilbert's 3rd problem asked about 3D. Max Dehn solved the problem: No. He proved you can't cut a regular tetrahedron into pieces to make a cube. Polyhedra of the same volume are Scissors Congruent iff they have the same Dehn Invariant. It turns out that the Engel-38 polyhedron has Dehn invariance 0.
There are 3D dissections. Hanegraaf's Rectangular Block of Size 211 to a Cube Dissection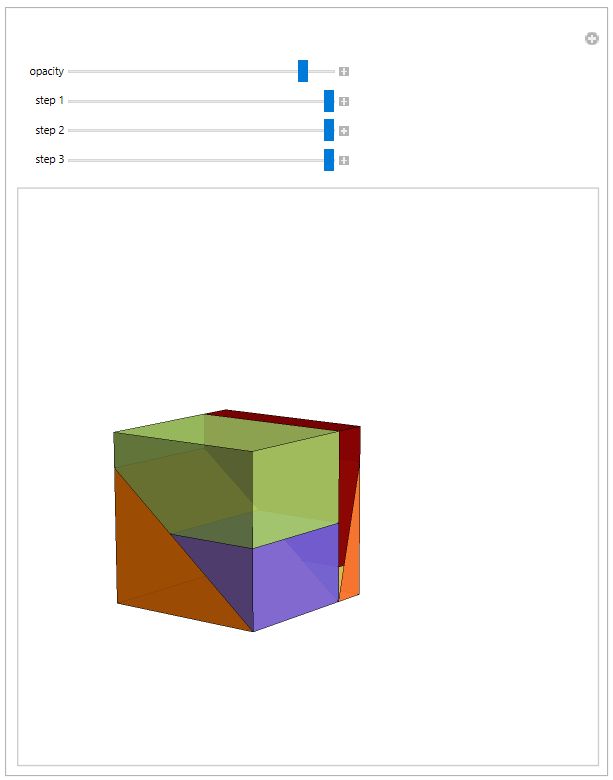 
Most dissections lack minimality proofs!
hexy = CirclePoints[6];
Graphics[{Line[Join[hexy, {hexy[[1]], hexy[[3]], Mean[{hexy[[1]], hexy[[3]]}], hexy[[2]]}]]}]
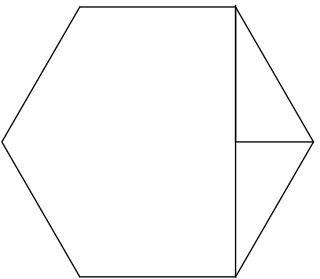
For example, above, a hexagon is divided into 3 pieces to make a rectangle. Is there a proof that 2 pieces isn't enough for cutting a hexagon into a rectangle?
