Message Boards Message Boards

0
|
1462 Views
|
3 Replies
|
3 Total Likes
View groups...
Share
Share this post:

Circular argumentation bug of Wolfram Alpha

Hongyi Zhao
Posted 11 months ago

I try to get the step-by-step solution for D[E^x, x] as follows:

WolframAlpha["D[E^x, x]", IncludePods -> "Input", 
 AppearanceElements -> {"Pods"}, PodStates -> {"Input__Show steps"}]

The result is given below:

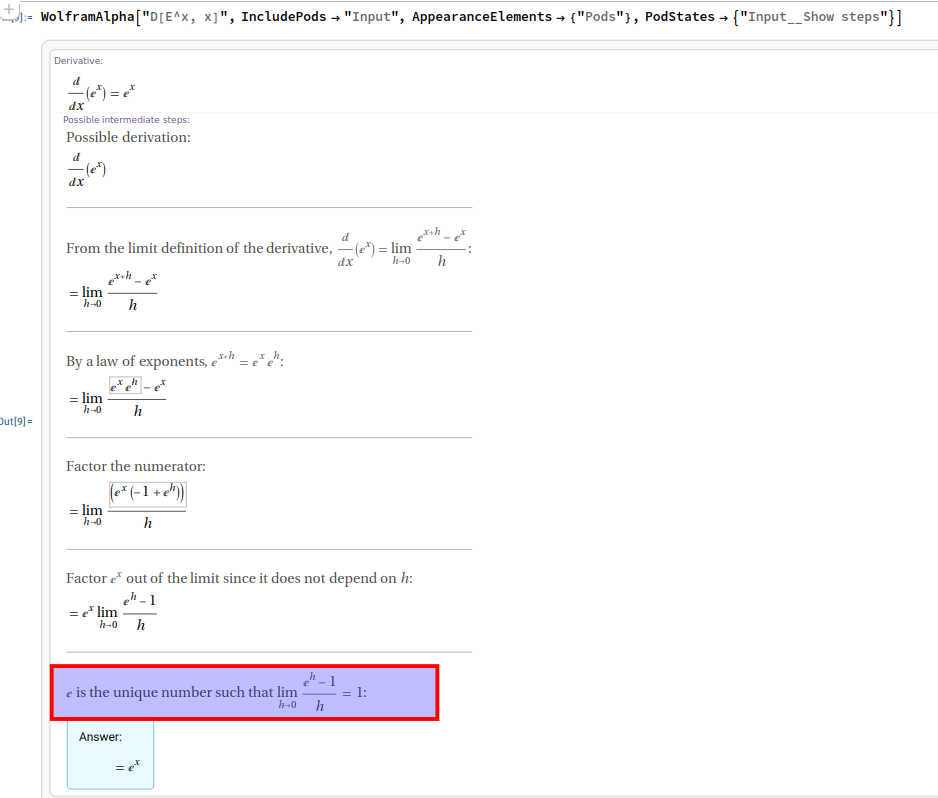
enter image description here

As you can see, this proof method is clearly trapped in the logic of circular argumentation, and therefore invalid.

Regards,
Zhao
POSTED BY: Hongyi Zhao
3 Replies
Sort By:
Hongyi Zhao
Hongyi Zhao
Posted 11 months ago

Do you expect W|A to give you all the steps up to the axioms of the real numbers?

Is this possible?
POSTED BY: Hongyi Zhao

I think that in this case W|A has given a pretty reasonable answer in this case. The limit Limit[(E^x - 1)/x, x -> 0]==1 is basic in every calculus textbook that I know of.

If you ask W|A the steps for the limit Limit[(E^x - 1)/x, x -> 0], it uses L'Hôpital's rule, which assumes that we know the derivative of the exponential. This would have been circular!
POSTED BY: Gianluca Gorni

It is not circular. It shows that if you know the derivative at x = 0 then you know it at any generic x. The derivative at x = 0 is a limit that is treated in all serious calculus textbooks. Do you expect W|A to give you all the steps up to the axioms of the real numbers?
POSTED BY: Gianluca Gorni
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract