I try to get the step-by-step solution for D[E^x, x] as follows:
WolframAlpha["D[E^x, x]", IncludePods -> "Input",
AppearanceElements -> {"Pods"}, PodStates -> {"Input__Show steps"}]
The result is given below:
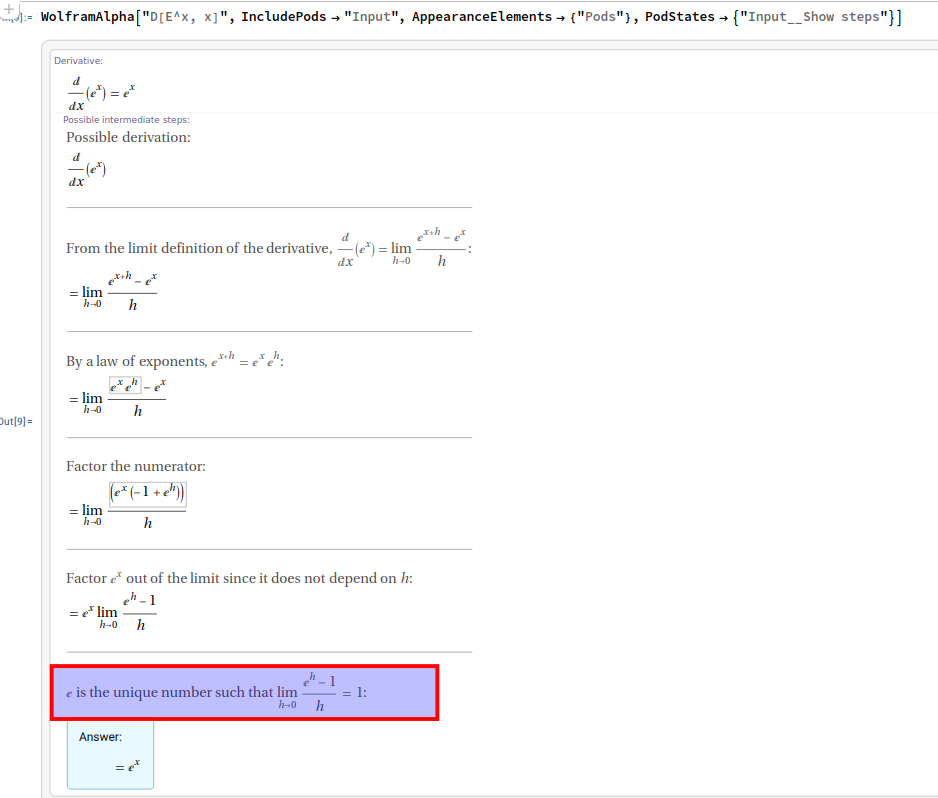
As you can see, this proof method is clearly trapped in the logic of circular argumentation, and therefore invalid.
Regards,
Zhao