Yes, this indeed seems a bit strange! On my system (13.3.0 for Linux x86 (64-bit) (June 3, 2023)) this does work:
FindMinimum[dsq[c[t], q], {t, .3}]
(* Out: {9.487787469526271`,{t\[Rule]0.5303065649428684`}} *)
but this answer is wrong!
Based on the good catch of @Gianluca Gorni consequently a correct result can be obtained like so:
FindMinimum[dsq[Threaded@c[t], q], {t, .3}]
As an aside: A completely different approach could use regions and friends:
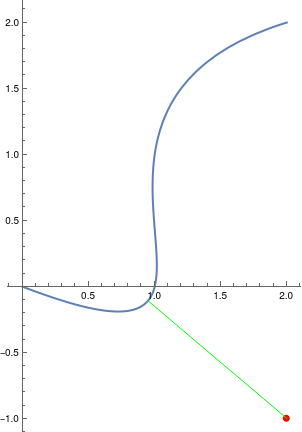
paramReg = DiscretizeGraphics[ParametricPlot[c[t], {t, 0, 1}]];
rnst = RegionNearest[paramReg, q];
ParametricPlot[c[t], {t, 0, 1}, Epilog -> {Red, PointSize[Large], Point[q], Green, Line[{q, rnst}]},
PlotRange -> {Automatic, {-1.1, Automatic}}]