So the error message you got usually means that the optimization algorith(nonlinearmodelfit) had some difficullty on converging to a solution.Here are a coupple points you could use to adress this issue. Initial Parameter Guesses: Ensure that the initial parameter guesses provided to NonlinearModelFit are reasonable and not too far from the expected values. This can help the optimization algorithm converge more effectively. Constraints and Bounds: Check if there are any constraints or bounds on the parameter values that need to be enforced during the fitting process. Providing appropriate constraints can sometimes help the optimization algorithm converge more reliably. Scaling and Rescaling: Consider rescaling your data and model equations if the parameters span several orders of magnitude. This can help improve numerical stability during optimization. Optimization Algorithm: Try using different optimization algorithms available in NonlinearModelFit by specifying the Method option. Some algorithms may perform better than others depending on the specific characteristics of your problem. Data Quality: Ensure that your data is of good quality and free from any outliers or numerical artifacts that could affect the fitting process. Model Complexity: Simplify your model if it is too complex or has too many parameters relative to the amount of data available. A simpler model may be easier to fit and less prone to convergence issues.

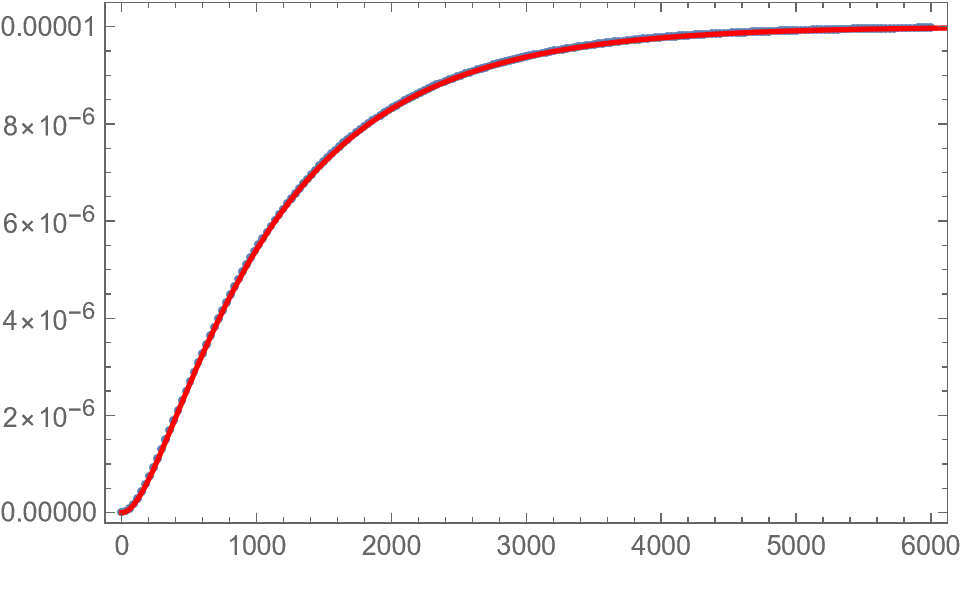
That message is a "warning" rather than an "error" as you see you still get a good fit. However, the underlying reason for the warning is that your model is overparametersized. If you look at the parameter correlation matrix you see the following:

nlf["CorrelationMatrix"]

The correlations for parameters Kt, K3, and Kmeno3 are all either +1 or -1 indicating that the model is overparameterized. Essentially there is just a single parameter that can be estimated among those 3 parameters:

model //. K3 Kt -> a (Kmeno3 + Kt) // FullSimplify
(* (c (a - a E^(-Kp x) + (-1 + E^(-a x)) Kp))/(a - Kp) *)

This more parsimonious model gives the exact same predictions as your original model but (likely) with fewer numerical issues. The only issue is that starting values can't be the same for a and Kp otherwise the denominator will start off as zero.

nlf2 = NonlinearModelFit[data, (c (a - a E^(-Kp x) + (-1 + E^(-a x)) Kp))/(a - Kp),
  {a, c, {Kp, 0.0001}}, x];
nlf2["BestFitParameters"]
(* {a -> 0.00500545, c -> 0.0000100002, Kp -> 0.000999561} *)
Show[ListPlot[data], 
 Plot[nlf[x], {x, 0, end}, PlotStyle -> Red, PlotRange -> All], 
 Frame -> True]