Manipulate[Plot[((a/(1 - b)) + (b/(1 - b))*c), {c, 0, 100},
PlotRange -> {{0, 100}, {0, 300}}, AxesOrigin -> {0, 0},
AxesLabel -> {"X", "Y"}], {{a, 30}, 0, 50}, {{b, .6}, .0000001, 1}, {{c, 90}, 0, 100}]
you cannot use the same variable c for that task: inside Plot[] as well as dynamic variable. Use x as running variable in the Plot[] instead.
An Epilog with the dynamic variable c does it
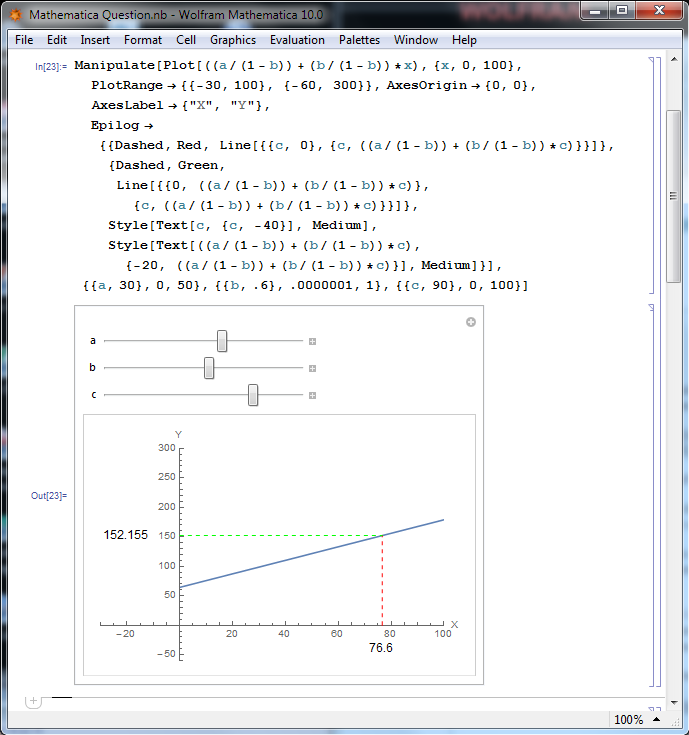
Manipulate[Plot[((a/(1 - b)) + (b/(1 - b))*x), {x, 0, 100},
PlotRange -> {{-30, 100}, {-60, 300}},
AxesOrigin -> {0, 0}, AxesLabel -> {"X", "Y"},
Epilog -> {{Dashed, Red, Line[{{c, 0}, {c, ((a/(1 - b)) + (b/(1 - b))*c)}}]},
{Dashed, Green, Line[{{0, ((a/(1 - b)) + (b/(1 - b))*c)}, {c, ((a/(1 - b)) + (b/(1 - b))*c)}}]},
Style[Text[c, {c, -40}], Medium],
Style[Text[((a/(1 - b)) + (b/(1 - b))*c), {-20, ((a/(1 - b)) + (b/(1 - b))*c)}], Medium]}],
{{a, 30}, 0, 50}, {{b, .6}, .0000001, 1}, {{c, 90}, 0, 100}]
One should also use a function definition in order not to be forced to type in the same function four times, the so called single point of definition principle.