I am still in the process of learning the Wolfram language. I have written the following two implementations of a function that finds all perfect numbers between the given range. The first implementation is how you may typically write such a function in a language such as c. The second version is my attempt at a more Mathematica version of the function.

PerfectSearch[from_Integer, to_Integer] := Module[
  {id = to},
  Flatten[Rest[Reap[While[id >= from,
      sum = 0;
      n = id - 1;
      While[n > 0,
       sum = sum + If[Mod[id, n] == 0, n, 0];
       n = n - 1];
      If[sum == id, Sow[id]];
      id = id - 1;
      ]
     ]
    ]
   ]
  ]

And

PerfectSearch2[from_Integer, to_Integer] := 
 Module[{testNumbers = Range[from, to]},
  MapThread[(If[#1 == #2, #1, (##) &[]]) &,
   {
    Map[
     Function[testNum,
      Total[
       Select[
        Map[
         Function[divisor, If[Mod[testNum, divisor] == 0, divisor, 0]],
         Range[testNum - 1]
         ],
        (# > 0) &
        ]
       ]
      ], 
     testNumbers
     ]
    ,
    testNumbers
    }
   ]
  ]

I generated timing information for these two implementations as follows

p1Timing = DeleteCases[
   Flatten[
    Table[
     Timing[
      PerfectSearch[1, n];
      ],
     {n, 2, 200}
     ]
    ]
   ,
   Null];

And

p2Timing = 
  DeleteCases[
   Flatten[Table[Timing[PerfectSearch2[1, n];], {n, 2, 200}]], Null];

This timing information is shown below

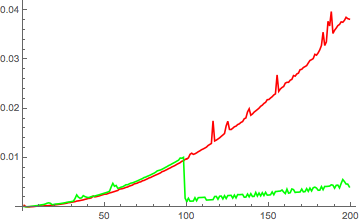
Can anyone explain to me what Mathematica is doing in the second version of the function. It appears that the two functions perform the same up until testing numbers of 100 and above. At this point the second version of the function takes significantly less time to calculate.

Feel free to point out any improvements in the code; As I say, I am still getting to grips with Mathematica.

Thanks in advance