MetalLink Project GitHub: https://github.com/s4m13337/MetalLink
Introduction
While working on some machine learning projects recently, I encountered a significant limitation: Mathematica’s inability to use Apple’s M-Series GPU for training neural networks. I had to resort to TensorFlow to speed up the training and and advance my tasks. However, my curiosity led me on a slight detour to investigate potential methods for utilizing Apple’s GPU within Mathematica.
Background
A quick internet search brings up this community post: https://community.wolfram.com/groups/-/m/t/2113522
The post is about 3 years old at the time of writing this and despite that, the absence of support for training neural networks on Apple’s GPU remains a puzzle. I am very certain that there is demand for this from many users of Mathematica such as myself. Maybe someone from Wolfram Research could illuminate about the current situation and future plans regarding this.
Nevertheless, I have been experimenting with Metal and various ways to access the GPU from Mathematica. In this post I summarize the different things I have found out. I had to refresh my knowledge on several low level functions in Mathematica since I have not worked with them with in a while. I also had to learn a bit of Objective C because as it is requisite for interfacing with Metal.
Design
Broadly, there are two components: a Metal program that is written in C and Objective C that can interacts with the GPU and there is a layer in Mathematica that establishes connection to this external program to exchange data.
The Metal side presents significant challenges as the documentation is hard to follow and does not contain any examples. I had to rely on heavy trial and errors to figure things out. This is the general workflow that needs to be done to pass data to the GPU for computation:
- Create a reference to the Metal device
- Load a library of kernels/compute shader functions
- Build a pipeline against the kernels/compute shader functions
- Create a command queue
- Create compute buffers/textures and load the data into them
- Define work grid size, threadgroup size and threads per thread group
- Push the compute buffers/textures into the command queue using a command buffer
- Commit the work to the GPU and wait till it completes the computation
Steps 1 to 4 can be done once and each of the objects can be reused. Step 5 is where the data obtained from Mathematica is loaded into a buffer and pushed to the GPU in Step 7. Step 6 is where the work is divided into groups for the GPU to process them in parallel. After computation, result is copied back to the program’s memory from the buffer and it is returned to Mathematica.
I am omitting several details on the terminologies mentioned above, as they are quite complex and would render this post excessively lengthy. Detailed explanations can be found in Metal's documentation. After implementing a basic version of the aforementioned program, I needed to interface it with Mathematica. Fortunately, the Mathematica side is relatively straightforward to implement. There are three well-documented options for this:
- ForeignFunctionInterface
- WSTP
- LibraryLink
ForeignFunctionInterface is a quick way to load an external program and play around with it. But this does not scale well for developing a bigger library. WSTP is a much more sophisticated framework and provides lot more features. But the main drawback here is that the external program loaded is connected to Mathematica only through a link and it consists of its own memory space. Any data from Mathematica must be pushed through the link and this becomes problem when pushing large amount of data. And this defeats the entire purpose of parallel computation.
LibraryLink is the most versatile solution. This requires the external program to be compiled as a dynamic library. When it is loaded into Mathematica, its memory space gets shared i.e. the external program has direct access to data in Mathematica.
Development
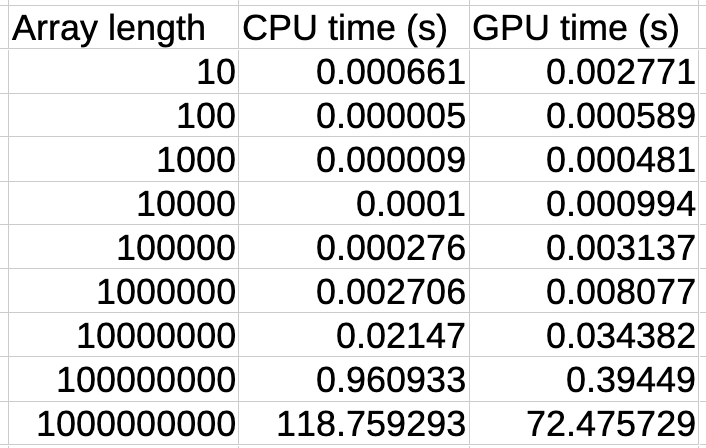
Taking inspiration from the existing CUDALink, I have named this library MetalLink (the most original name I could come up with). To begin with, I developed a simple function that just adds two lists in parallel. Although a trivial task, it serves as a good benchmark to assess the efficiency of GPU computation. And to really put pressure on the GPU, each list consisted of 1 billion items. The initial results I obtained where a bit disappointing, however: Addition on Mathematica took close to 2 minutes (118 seconds to be exact), where as on the GPU, it took 5 minutes - more than twice the time.
Upon closer inspection during debugging, I found that the actual computation time on the GPU was less than a second. The majority of the time was consumed in memory allocation and data writing to the buffer. To address this bottleneck, I delved deep into the GPU's architecture to devise a method for accelerating these processes. Subsequently, I implemented a technique to asynchronously chunk the data from Mathematica and create buffers of these chunk sizes. This optimization significantly enhanced performance, reducing the time for adding two lists to just over a minute (72 seconds, to be exact). That's nearly a 50% improvement in speed.
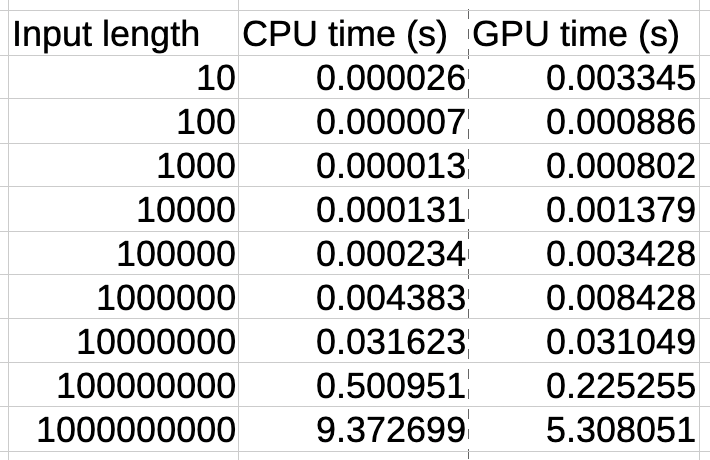
Continuing with my development efforts, another function I created is the Map function, inspired by the existing CUDAMap, which I aptly named MetalMap. The table below summarizes the computation times for applying the Sin function to lists of various length:
Conclusion
Furthermore, to explore the image processing capabilities, I have developed a function that creates a negative of an Image. Although it technically works, its optimization is still a work in progress. I am still figuring out ways to optimize but the plan is to slowly extend the capabilities and make the library ready for general purpose GPU computation on Apple silicon devices. Perhaps one day, this library will mature to the point where I can finally just set the option “TargetDevice” -> “GPU” on the Apple silicon devices to train Neural Networks.
The project is available at https://github.com/s4m13337/MetalLink and any contributions are welcome.
Remarks
Note 1: All the tests were done on a M1 chip MacBook with 8 GB RAM. This device uses a unified memory architecture and the maximum memory shared with the GPU is about 5 GB. Going beyond 5 GB requires further low level memory management strategies.
Note 2: Just out of curiosity, I also tried testing the library on a MacBook with NVIDIA GPU. Although it works, subsequent computations produce garbage results. This is probably due to incompatibilities in the automatic reference counter / garbage collector of the compiler used.