From the initial attempt to fit the data I gather that Ald is the benzaldehyde. The data has numerous y values for the same x values though. Was this from multiple experiments? If so, it would make sense to perhaps ,average those y values.
Maybe more important is the question of what exactly is needed. Is it the DE solution? Or identification of the parameter value for kzero? If the latter, I would suggest using ParametricNDSolve, especially if there are known values for initial concentrations. One could proceed like so, using data from this post's notebook.
Average the values:
newdatabenz =
Map[{#[[1, 1]], Mean[#[[All, 2]]]} &, SplitBy[databenz, First]]
(* Out[118]= {{0., 0.0174805}, {361., 0.0102426}, {659.,
0.006913}, {944., 0.00504}, {1241., 0.00391667}, {1528.,
0.0037}, {1825., 0.00334333}} *)
Get a parametricized numeric ODE solution function for the aldehyde.
solP = ParametricNDSolveValue[{Ald'[t] == -kzero Ald[t] Hydr[t],
Hydr'[t] == -kzero Ald[t] Hydr[t],
Prod'[t] == kzero Ald[t] Hydr[t], Ald[0] == .026, Hydr[0] == .025,
Prod[0] == 0}, Ald, {t, 0, 2000}, kzero];
Find a fit to the averaged data:
(* kzfit =
FindFit[newdatabenz, solP[kzero][t], {{kzero, .1}}, t]
Out[121]= {kzero -> 0.181871} *)
Plot the solution curve and data points:
kzval = kzero /. kzfit;
Show[ListPlot[newdatabenz, PlotStyle -> PointSize[0.025]],
Plot[solP[kzval][t], {t, 0, 1825}, PlotRange -> All],
PlotRange -> All]
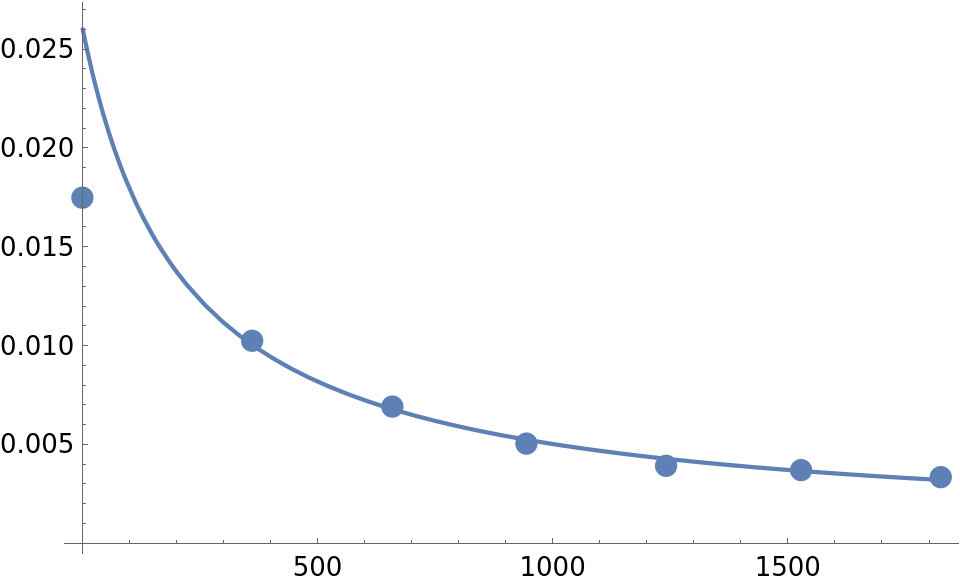
Not bad except for the first point.