Note that:
Reduce[
n1^2 k0^2 - [Beta]^2 > 0 && [Beta]^2 - n2^2 k0^2 > 0]
gives
-6.1282 10^6 < [Beta] < -6.10726 10^6 ||
6.10726 10^6 < [Beta] < 6.1282 10^6
so any places where p and q are both real are located in one of these ranges.
So go ahead and plot the full expression (i.e., the left hand side minus the right hand side) in, for example, the second range:
Plot[((1/2 (BesselJ[0, p a] - BesselJ[2, p a]))/(p BesselJ[1,
p a]) + (1/
2 (-BesselK[0, q a] - BesselK[2, q a]))/(q BesselK[1,
q a])) ((1/2 (BesselJ[0, p a] - BesselJ[2, p a]))/(p BesselJ[
1, p a]) +
n2^2/n1^2 (1/2 (-BesselK[0, q a] - BesselK[2, q a]))/(q BesselK[
1, q a])) - (1)^2/
a^2 (1/p^2 + 1/q^2) (1/p^2 + n2^2/n1^2 1/q^2), {[Beta],
6.107256118578557`*^6, 6.1282000696024895`*^6}]
giving
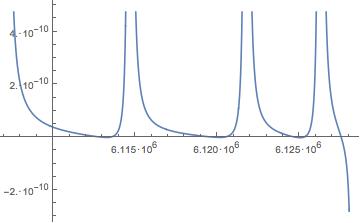
So there appear to be some zeros in this region. And one can use this plot to select a starting point for the FindRoot function as in:
FindRoot[((1/2 (BesselJ[0, p a] - BesselJ[2, p a]))/(p BesselJ[1,
p a]) + (1/
2 (-BesselK[0, q a] - BesselK[2, q a]))/(q BesselK[1,
q a])) ((1/
2 (BesselJ[0, p a] - BesselJ[2, p a]))/(p BesselJ[1, p a]) +
n2^2/n1^2 (1/
2 (-BesselK[0, q a] - BesselK[2, q a]))/(q BesselK[1,
q a])) - (1)^2/
a^2 (1/p^2 + 1/q^2) (1/p^2 + n2^2/n1^2 1/q^2) == 0, {[Beta],
6.12 10^6}]
giving
{[Beta] -> 6.11989[CenterDot]10^6}
But there are several solutions around here (to the accuracy of the FindRoot computation), some possibly elsewhere on the complex plane.
using 6.125 10^6 as the seed value gives a root at
{[Beta] -> 6.1248[CenterDot]10^6}