Hello, I’m trying to solve an optimization model for growing items based on a paper that uses Excel Solver to obtain the optimal solution. The model has two decision variables: n (frequency of shipments) and T (retailer's replenishment cycle). The paper provides the following equations and parameter values: 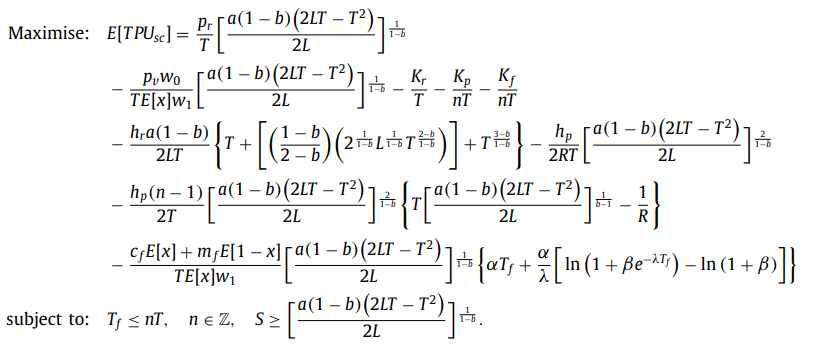

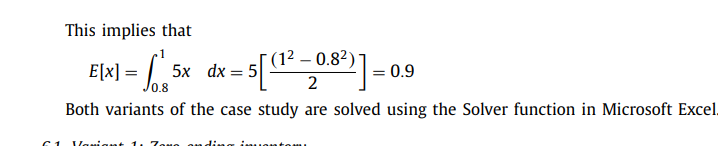
The optimal values from the paper are: - n(shipment frequency) = 20 - T(retailer's replenishment cycle) = 1.62 days - Total profit = 421.14 ($/day)
Right now, I am attempting to solve the same problem in Mathematica, but I’m encountering an issue when using FindMaximum to determine the optimal values for both n and T. Here is the code I am using to find the optimal solution of both n and T
Clear["Global`*"]
L = 4;
w = 0.064;
ww = 2;
R = 250;
Kf = 750;
cf = 0.1;
m = 0.2;
Kp = 500;
hp = 0.05;
Kd = 100;
h = 0.1;
g = 6.87;
q = 0.12;
a = 80;
b = 0.2;
pv = 1;
pf = 2;
pr = 5;
z = 120;
x = 0.9;
s = 0.2;
Tf = - (Log[1/z (k/ww - 1)]/q);
F[d_, n_] =
pr/d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - (pv w)/(
d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - Kd/d -
Kp/(n d) - Kf/(
n d) - (h a (1 - b))/(
2 L d) (d + (((1 - b)/(
2 - b)) (2^(1/(1 - b)) L^(1/(1 - b)) d^((2 - b)/(1 - b))) +
d^((3 - b)/(1 - b)))) -
hp/(2 R d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(1 - b)) - (
hp (n - 1))/(2 d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(
1 - b)) (d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - 1/
R) - (cf x + m s)/(d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(
1/(1 - b)) (g Tf + g/q (Log[1 + z E^(-q n Tf)] - Log[1 + z]));
FindMaximum[{F[d, n], d > 0}, {d, n}]
However, I encounter an error in my code:
FindMaximum::nrnum: The function value 598.228 +11.0638 (57.25 (-Log[121]+Log[1+Times[<<2>>]])-57.25 Log[1/120 (-1+Times[<<2>>])]) is not a real number at {d,n} = {0.999994,1.}.
FindMaximum::grad: Evaluation of the gradient of function Experimental`NumericalFunction[{Hold[-(-(100/d)+(66.7933 (Times[<<2>>]+<<1>>)^1.25)/d-(0.0181019 (<<1>><<1>>^2.5)/d-(0.8 <<1>>)/d-(<<18>> <<1>> <<1>> (-1+n))/d-1250/(d n)-(0.971703 (<<1>>)^1.25 (57.25 Plus[<<2>>]-57.25 Log[<<1>>]))/d)],Block},<<4>>,{<<1>>}] failed at {1.,1.}.
After that, I try to just find the optimal solution of T only by setting the n value with the optimal value from the paper which is 20. However, the total profit and the value of T I obtain are different from the results in the paper. Here is the code I use for this :
Clear["Global`*"]
L = 4;
w = 0.064;
ww = 2;
R = 250;
Kf = 750;
cf = 0.1;
m = 0.2;
Kp = 500;
hp = 0.05;
Kd = 100;
h = 0.1;
g = 6.87;
q = 0.12;
a = 80;
b = 0.2;
pv = 1;
pf = 2;
pr = 5;
z = 120;
n = 20;
x = 0.9;
s = 0.2;
Tf = - (Log[1/z (g/ww - 1)]/q);
F[d_] = pr/d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - (pv w)/(
d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - Kd/d -
Kp/(n d) - Kf/(
n d) - (h a (1 - b))/(
2 L d) (d + (((1 - b)/(
2 - b)) (2^(1/(1 - b)) L^(1/(1 - b)) d^((2 - b)/(1 - b))) +
d^((3 - b)/(1 - b)))) -
hp/(2 R d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(1 - b)) - (
hp (n - 1))/(2 d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(
1 - b)) (d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - 1/
R) - (cf x + m s)/(d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(
1/(1 - b)) (g n Tf + g/q (Log[1 + z E^(-q n Tf)] - Log[1 + z]));
FindMaximum[{F[d], d > 0}, d]
The result I obtained are : Total profit = -27730 and T = 0.029
Could anyone help me understand why I am getting different results in Mathematica compared to the paper, even after using the same parameter values and the optimal value for n from the paper? Are there any potential issues with the way I’m using FindMaximum or something I might be overlooking in the optimization setup?
In case it was needed, here is the link of the paper : https://www.sciencedirect.com/science/article/abs/pii/S0307904X20306120 (I also attached the paper below)
Any insights would be greatly appreciated! Thank you!
 Attachments:
Attachments: