Message Boards Message Boards

Unexpected result from DSolve? (Version dependence)

Could you help me to understand the following?

In[1]:= $VersionNumber

Out[1]= 14.

In[2]:= DSolve[{2.3*r''[t]==1-r'[t],r[0]==0,r'[0]==0},r[t],t]//FullSimplify

Out[2]= {{r[t] -> -2. + 2.3 E^(-0.434783 t)}}

In[3]:= DSolve[{m*r''[t]==f-r'[t],r[0]==0,r'[0]==0},r[t],t]/.{m->2.3,f->1}//FullSimplify

Out[3]= {{r[t] -> -2.3 + 2.3 E^(-0.434783 t) + t}}

2.3 seems to be a magic number. Is this a bug?

(2024-10-23 ADD) Thank you for replies. I found version dependence. I report the result in the following by using Gianluca Gorni's DiscretePlot.

derivativeAtZero[a_] := DSolveValue[{a*r''[t] == 2 - r'[t], r[0] == 0, r'[0] == 0}, r, t]'[0];
fncAtZero[a_] := DSolveValue[{a*r''[t] == 2 - r'[t], r[0] == 0, r'[0] == 0}, r, t][0];
DiscretePlot[{fncAtZero[a], derivativeAtZero[a]}, {a, Subdivide[1., 3, 200]}, PlotLabel -> $VersionNumber]

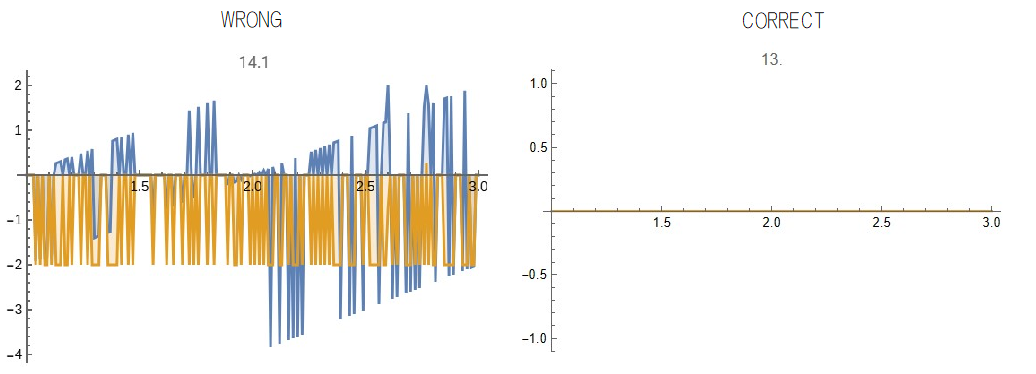
enter image description here

Correct answer(right figure) : version=13.1, 13.0, 12.2?

Wrong answer(left figure) : version=14.1, 14

(2024-10-23 ADD2) Thanks to Michael Rogers' reply, I noticed a way to reveal version-dependent numerical instability.

The equation 2.3 r’’(t)=1 - r’(t) can be generalized to 2.3 r’’(t)=exp(k t) - r’(t). The following command

DSolveValue[{2.3*r''[t]==Exp[k*t]-r'[t],r[0]==0,r'[0]==0},r[t],t]//FullSimplify//FullForm//Print

gives version-dependent outputs

version 14: Times[-1,Plus[0.4347826086956521`,Times[-0.43478260869565216`,Power[E,Times[k,t]]],Times[0.9999999999999999`,k],Times[-0.9999999999999999`,Power[E,Times[-0.43478260869565216`,t]],k]],Power[Plus[Times[0.43478260869565216`,k],Times[1.`,Power[k,2]]],-1]]
version 13: Times[-1,Plus[0.4347826086956522`,Times[-0.4347826086956522`,Power[E,Times[1.`,k,t]]],Times[1.`,k],Times[-1.`,Power[E,Times[-0.4347826086956522`,t]],k]],Power[Plus[Times[0.4347826086956522`,k],Power[k,2]],-1]]

One can see small deviations of the same number 0.4347..., that is 1/2.3. In version 14, the numerical instability 0.4347826086956521 - 0.43478260869565216 = 5.55112*10^-17 appears in the solution shown by Michael Rogers.

This numerical instability depends on the number 2.3. For example, we obtain the correct answer and no numerical instability for the number 2.31 even if we use version 14.

DSolveValue[{2.31*r''[t]==1-r'[t],r[0]==0,r'[0]==0},r[t],t]//FullSimplify
(*
-2.31 + 2.31 E^(-0.4329 t) + 1. t
*)
DSolveValue[{2.31*r''[t]==Exp[k*t]-r'[t],r[0]==0,r'[0]==0},r[t],t]//FullSimplify//FullForm//Print
(*
Times[-1,Plus[0.4329004329004329`,Times[-0.4329004329004329`,Power[E,Times[k,t]]],Times[1.`,k],Times[-1.`,Power[E,Times[-0.4329004329004329`,t]],k]],Power[Plus[Times[0.4329004329004329`,k],Power[k,2]],-1]]
*)

(2024-10-24 ADD) In conclusion, I have understood that this unexpected result from DSolve was due to the numerical instability of a round-off error existing only in latest versions(>=14) of Mathematica. In the following, I report a new magic number with large round-off error (worst case), aWorst, by showing version-dependent solutions of $a\times v'(t)=e^{k t} - v(t) $ with using the following commands.

aWorst=5750000000002614783/2500000000000000000;
eq[a_,k_]:=a*v'[t]==Exp[10^-k*t]-v[t];
check[a_]:=Block[{},
Print[TraditionalForm[eq[a,k]],"\n a=",FullForm[a]," with Version",$VersionNumber,"\n",
TableForm[{#,DSolveValue[eq[a,#],v[t],t]}&/@Range[20],TableHeadings->{None,{"k","v(t)"}}]]];
check[2.3]
check[N[aWorst]]
check[2.31]

The result for version 14 shows unexpected round-off error while that for version 13 is reasonable.

enter image description here enter image description here To avoid it, one can use the following quick hack.

dSolveValue[eqs_,fnc_,arg_]:=Expand[DSolveValue[Rationalize[eqs,0],fnc,arg]]/.n_?NumberQ:>N[n];

I guess something has happened during the version update, and it might be not intended by the developer. I will report this to Wolfram support. I would like to thank you for your help and replies.
POSTED BY: Isao Maruyama
7 Replies
Sort By:

I see. However, I have never seen before this kind of incorrect numerical answer in Mathematica. For example, maxima's desolve has the auto-rationalize trick.

enter image description here

I thought Mathematica did it in a more elegant way than maxima. If DSolve requires exact numbers only, then I have to rewrite my teaching materials...
POSTED BY: Isao Maruyama

Thanks. It works also for me. A quick hack is the following;

dSolve[eqs_, fnc_, arg_] := DSolve[Rationalize[eqs], fnc, arg];
dSolve[{2.3*r''[t] == 1 - r'[t], r[0] == 0, r'[0] == 0}, r[t], t]
POSTED BY: Isao Maruyama

Thank you for your detailed analysis about numerical instability.

As you mentioned, I could get the correct answer by using the higher order system in version 14.0, which is magic for me:

DSolve[{D[2.3*r''[t] == 1 - r'[t], t], 2.3*r''[0] == 1 - r'[0], r[0] == 0, r'[0] == 0}, r[t], t] // Simplify

And, I noticed that Mathematica ver.13.0 gives different (correct) answer:

TracePrint[ DSolve[{2.3*r''[t] == 1 - r'[t], r[0] == 0, r'[0] == 0}, r[t],   t], _DSolve`DSolveBoundaryValueProblem, TraceForward -> True,  TraceInternal -> True]
(*
DSolve`DSolveBoundaryValueProblem[DSolve,DSolve`DSolveParserDump`result,DSolve`DSolveParserDump`initial,DSolve`DSolveParserDump`ctab,DSolve`DSolveParserDump`independents]

DSolve`DSolveBoundaryValueProblem[DSolve,{{r[t]->1. t-2.3 E^(-0.434783 t) Subscript[\[ConstantC], 1]+Subscript[\[ConstantC], 2]}},{r[0]==0,(r^\[Prime])[0]==0},{Subscript[\[ConstantC], 1],Subscript[\[ConstantC], 2]},{t}]

{r[t] -> 
   1. E^(-0.434783 t) (2.3 - 2.3 E^(0.434783 t) + 
      1. E^(0.434783 t) t)}}
*)
POSTED BY: Isao Maruyama

The original ODE is equivalent to a homogeneous 3rd-order ODE with a repeated root:

inflated = {D[2.3*r''[t] == 1 - r'[t], t],
   2.3*r''[t] == 1 - 0, r[0] == 0, r'[0] == 0}
(*  {2.3` r'''[t] == -r''[t], 2.3` r'[t] == 1, r[0] == 0, r'[0] == 0}  *)

First@inflated /. r -> Function[t, Exp[L t]] /. t -> 0 // Solve
(*  {{L -> -0.434783}, {L -> 0.}, {L -> 0.}}  *)

A repeated root is numerically unstable — any round-off error is likely to split the root in two. This is what happens in the procedure used by DSolve to solve the OP's nonhomogeneous 2nd-order ODE:

TracePrint[
 DSolve[{2.3*r''[t] == 1 - r'[t], r[0] == 0, r'[0] == 0}, r[t], t],
 _DSolve`DSolveBoundaryValueProblem,
 TraceForward -> True,
 TraceInternal -> True]
(*
DSolve`DSolveBoundaryValueProblem[DSolve,  
 DSolve`DSolveParserDump`result, DSolve`DSolveParserDump`initial, 
 DSolve`DSolveParserDump`ctab, DSolve`DSolveParserDump`independents]

DSolve`DSolveBoundaryValueProblem[DSolve, 
 {{r[t] -> 1.80144*10^16 E^(5.55112*10^-17 t) - 2.3 E^(-0.434783 t) C[1] + C[2]}},
 {r[0] == 0, Derivative[1][r][0] == 0}, {C[1], C[2]}, {t}]

{{r[t] -> E^(-0.434783 t) (2.3 - 2. E^(0.434783 t))}}
*)

The number 5.55112*10^-17 in the first exponential term is a round-off error of 2.^-54 and 1.80144*10^16 is its reciprocal. If C[2] were -1.80144*10^16, they the two terms together would be approximately t (for small enough t). That would make this solution equivalent to the correct, exact solution.

The following shows the steps from the general to the particular solution, verifying the some of the description above:

gensol = DSolve[{23/10.*r''[t] == 1 - r'[t]}, r[t], t]
gensolFN = DSolve`DSolveToPureFunction[gensol]
(*
{{r[t] -> 
   1.80144*10^16 E^(5.55112*10^-17 t) - 2.3 E^(-0.434783 t) C[1] + C[2]}}

{{r -> Function[{t}, 
    1.80144*10^16 E^(5.55112*10^-17 t) - 2.3 E^(-0.434783 t) C[1] + C[2]]}}
*)

csol = Solve[{r[0] == 0, r'[0] == 0} /. First@gensolFN, {C[1], C[2]}]
gensol /. First@csol // Factor
% // Simplify
(*
{{C[1] -> -1., C[2] -> -1.80144*10^16}}

{{r[t] -> 1. E^(-0.434783 t) (2.3 - 2. E^(0.434783 t))}}

{{r[t] -> -2. + 2.3 E^(-0.434783 t)}}
*)

Round-off error and its effects is normally considered one of the risks of working with floating-point numbers. As others have pointed out, DSolve[] is an exact solver, and it has (probably) not been designed to be careful with approximate floats. OTOH, it solves the higher order system without trouble:

DSolve[inflated, r[t], t] // Simplify
(*  {{r[t] -> -2.3 + 2.3 E^(-0.434783 t) + 1. t}}  *)

Evidently, it's using a different sequence of steps, but one should expect that, given one is homogeneous and the other nonhomogeneous. You could report it to Wolfram support. They might be able to improve DSolve[].
POSTED BY: Michael Rogers

Very strange, the result is totally discontinuous in the parameter:

derivativeAtZero[a_] := 
  DSolveValue[{a*r''[t] == 2 - r'[t], r[0] == 0, r'[0] == 0},
     r, t]'[0];
DiscretePlot[derivativeAtZero[a], {a, Subdivide[1., 3, 200]}]
POSTED BY: Gianluca Gorni

DSolve, Solve are symbolic solvers,works correct with only exact numbers.

Exact numbers have infinity precision.

    DSolve[{23/10*r''[t] == 1 - r'[t], r[0] == 0, r'[0] == 0}, r[t], 
      t] // Simplify
    DSolve[{m*r''[t] == f - r'[t], r[0] == 0, r'[0] == 0}, r[t], 
       t] /. {m -> 23/10, f -> 1} // Simplify

   (*{{r[t] -> -(23/10) + 23/10 E^(-10 t/23) + t}}*)
   (*{{r[t] -> -(23/10) + 23/10 E^(-10 t/23) + t}}*)

Regards M.I.
POSTED BY: Mariusz Iwaniuk
Bill Nelson
Bill Nelson
Posted 1 month ago

Try changing 2.3 to 23/10 and remove the FullSimplify and see if you can correctly manually simplify the result and get the same thing that FullSimplify gives you.

Then try substituting the solution into each of your three original equations and use D to calculate each needed derivative and see if the result is True in every case.

Both those appear to work for me.
POSTED BY: Bill Nelson
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract