So it sounds like B is a 3xn matrix, where each column {xj,yj,zj} is the components of some separable function fj[x,y,z] = xj + yj + zj?

I'm going to slightly change the definition instead and have a length n vector of functions of x,y,z {f1[x,y,z], ... , fn[x,y,z]}

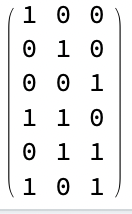
I first create a matrix A where a 1 denotes "differentiate with this variable":

vars = {x, y, z};
nVars = Length@vars;

A = With[{id = IdentityMatrix[nVars]},
   id~Join~(id + RotateLeft[id])];
A // MatrixForm

Then calculate the Jacobian and transpose. Here for example with 2 functions:

n = 2;
funs = Table[Symbol["f" <> ToString[i]] @@ vars, {i, n}];
J = Outer[D, funs, vars] // Transpose;
J//MatrixForm

Then dot A with the transposed Jacobian J:

(A . J) // MatrixForm

We can alternatively do this without naming the variables, and just specifying which argument we want to differentiate with using A:

ClearAll["`*"]
nVars = 3;
id = IdentityMatrix[nVars];

A = id~Join~(id + RotateLeft[id]);

n = 2;
funNames = Symbol["f" <> ToString[#]] & /@ Range[n];
J = Outer[Derivative[Sequence @@ #1][#2] &, id, funNames, 1, 1];

A . J // MatrixForm

There is likely a much cleaner way to do this using Inner, but I haven't figured out a nice way of doing it yet.

Hi David,

Thank you very much for your answer!

Matrix b is something like that =>

I will look into the answer you gave me and let you know if this works for me. Thanks!