Hi J. M.
Thanks for sharing the very interesting post with the lovely Japanese Anime.
1. Check another japanese blog 美しすぎるハートの数式
The equation of (x^2+y^2-1)^3==4x^2 y^3 comes from Eugen Beutel
in a German math book Algebraische Kurven in 1909. It's probably the earliest heart curve, except Cardioid. It keeps to been an order-6 algebraic equation, even it has been modified or simplified a little bit.
2. Yukimura's unfinished polar equation
I modified Yukimura's unfinished polar equation with following steps. I regard it as an ellipse with long-axis along 45 °, then reflect its half curve along Y axis. Finally, I combine two half-curves into one heart curve.
With[{t=4.32},PolarPlot[(4+Sin[t])/Sqrt[1-Cos[\[Theta]-Pi/2]Abs[Sin[\[Theta]-Pi/2]]],{\[Theta],0,2\[Pi]}]]
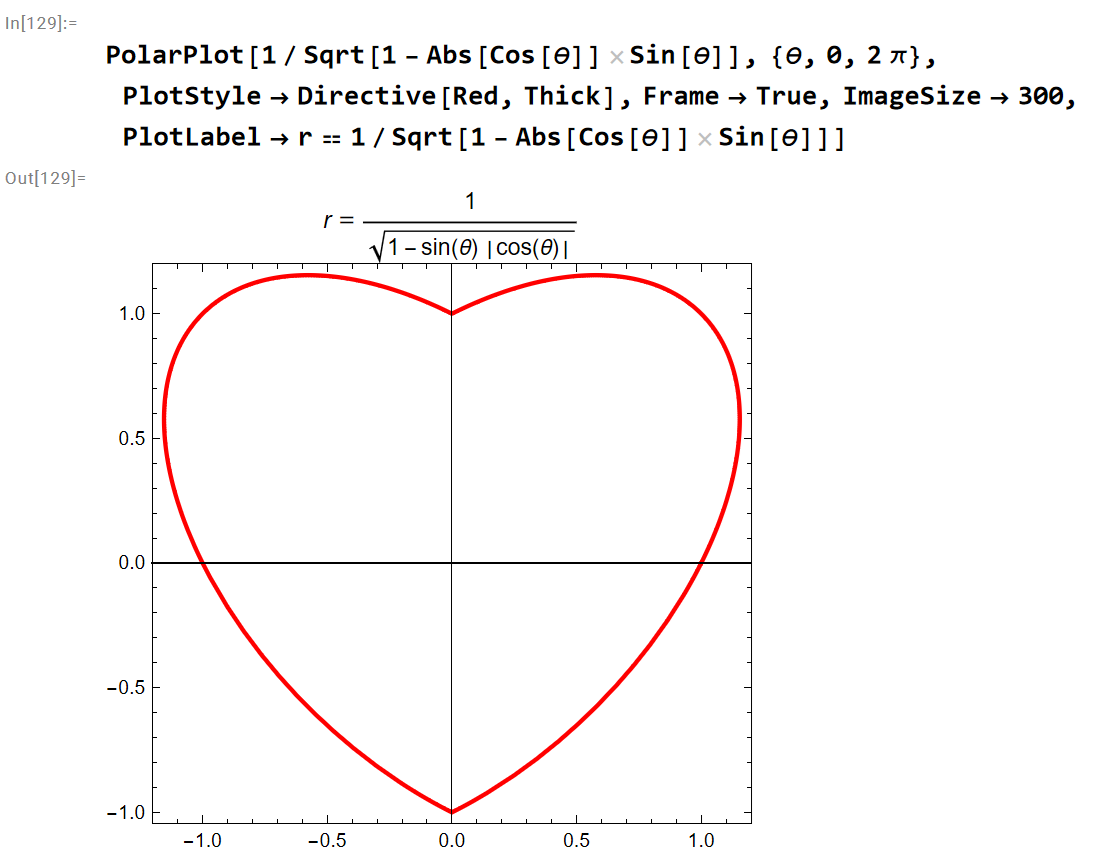
The denominator (4+Sin[t], t=4.32) is just a constant in the equation, so I replaced it with 1 for a neat form.
PolarPlot[1/Sqrt[1-Abs[Cos[\[Theta]]]Sin[\[Theta]]],{\[Theta],0,2\[Pi]}]