Your code is almost correct :)

residualPlot[data_, function_, {xmin_, xmax_}, opts : OptionsPattern[]] := 
 Show[ListPlot[{data, Table[{x, function[x]}, {x, data[[All, 1]]}]}, 
   Filling -> {1 -> {2}}, FillingStyle -> {Red, Green}, PlotMarkers -> {{"*", Large}, ""}, opts], 
  Plot[function[x], {x, xmin, xmax}]]

However, once you have defined the function above, let's say:

f[x_] := 3 - .25 x + .125 x^2 

there is not need to include it as an argument of the residualPlot function:

residualPlot[data_, {xmin_, xmax_}, opts : OptionsPattern[]] := 
 Show[ListPlot[{data, Table[{x, f[x]}, {x, data[[All, 1]]}]}, 
   Filling -> {1 -> {2}}, FillingStyle -> {Red, Green}, PlotMarkers -> {{"*", Large}, ""}, opts], Plot[f[x], {x, xmin, xmax}]]

Here is how it works:

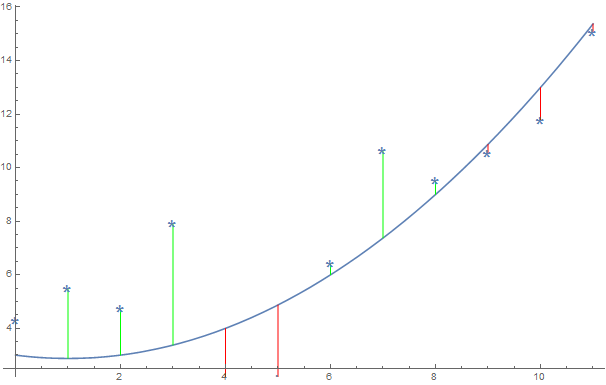
Looks fine, but you may encounter a problem when plotting the same function with data which is not generated from xmin to xmax. There is a trick which allows you to deal with it without specifying the {ymin, ymax} in the PlotRange - you can just change the places of the plots:

residualPlot[data_, {xmin_, xmax_}, opts : OptionsPattern[]] := 
 Show[Plot[f[x], {x, xmin, xmax}], 
  ListPlot[{data, Table[{x, f[x]}, {x, data[[All, 1]]}]}, Filling -> {1 -> {2}}, 
    FillingStyle -> {Red, Green}, PlotMarkers -> {{"*", Large}, ""}],opts]

then the LogPlot will inherit the "properties" of the first Plot (but now you need to change the "opts" to Plot[], or better to Show[]).

That works, only correction needed was to give the argument x to the function function

Clear[residualPlot]
residualPlot[data_, function_, {x_, xmin_, xmax_}, opts___Rule] := 
 Show[ListPlot[{data, Table[{x, function[x]}, {x, data[[All, 1]]}]}, 
   Filling -> {1 -> {2}}, FillingStyle -> {Red, Green}, 
   PlotMarkers -> {"*", ""}, opts], Plot[function[x], {x, xmin, xmax}]]

Clear[theFct]
theFct[x_] := 3 - .25 x + .125 x^2

someData = 
  Table[{x, theFct[x] + RandomReal[{-1, 4/5}]}, {x, 0, 4, 0.1}];

residualPlot[someData, theFct, {x, 0, 4}]