This is not an exact equation
In[160]:= Clear[a0, a1, a2, a3, a4]
a0[r_] := b
a1[r_] := 2 b/r
a2[r_] := (a - b/r)
a3[r_] := (b + a r^2)/r^3
a4[r_] := 0
In[167]:= (-1)^4 D[a0[r], {r, 4}] + (-1)^3 D[a1[r], {r, 3}] + (-1)^2 D[a2[r], {r, 2}] + (-1)^1 D[a3[r], {r, 1}] + a4[r] // Simplify
Out[167]= (15 b - 2 b r + a r^2)/r^4
unless a and b are both zero. So one cannot reduce the order of the equation. Nevertheless - in experimental mode - set v[r] = r^3 w'[r] to arrive at
(* Ansatz: w'[r] = r^3 v[r] *)
(b + a r^2) v[r] + (a - b/r) D[r^3 v[r], r] +
2 b/r D[r^3 v[r], {r, 2}] + b D[r^3 v[r], {r, 3}] // Simplify
(b (19 - 3 r) + 4 a r^2) v[r] + r ((30 b - b r + a r^2) v'[r] + b r (11 (v''[r] + r v'''[r]))
for this new equation it is possible to get some inhomogenous solutions (for simple inhomogenities) but it seems impossible to find one which is finite at r = 0.
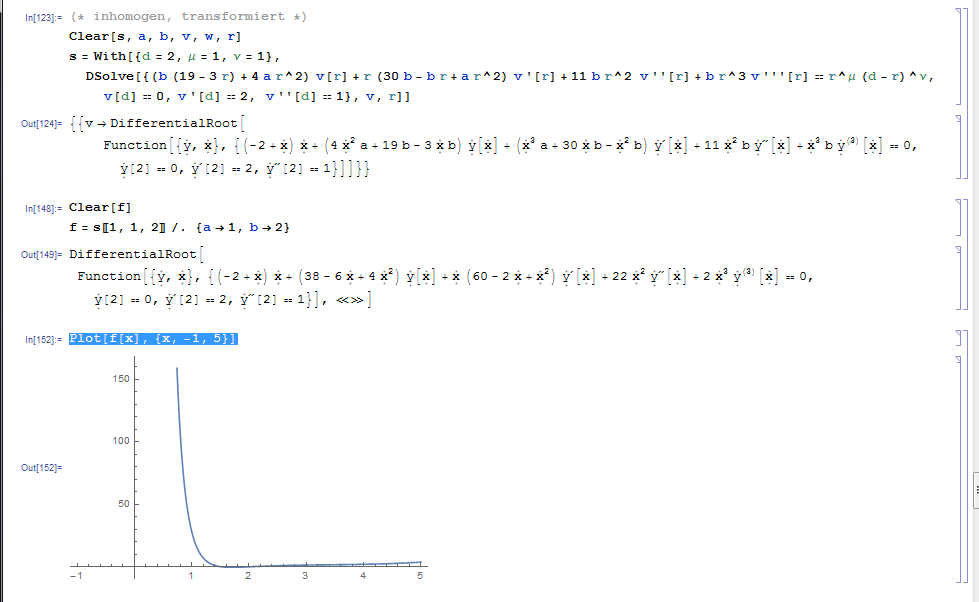
(* inhomogen, transformiert *)
Clear[s, a, b, v, w, r]
s = With[{d = 2, \[Mu] = 1, \[Nu] = 1},
DSolve[{(b (19 - 3 r) + 4 a r^2) v[r] +
r (30 b - b r + a r^2) v'[r] + 11 b r^2 v''[r] +
b r^3 v'''[r] == r^\[Mu] (d - r)^\[Nu], v[d] == 0, v'[d] == 2,
v''[d] == 1}, v, r]]
Clear[f]
f = s[[1, 1, 2]] /. {a -> 1, b -> 2}
Plot[f[x], {x, -1, 5}]
Things which did not work
- prescribing a finiteness condition at r = 0
- get solutions to the inhomogenous equation in less than an hour (computation aborted) with NDSolve
- get solutions to the original equation for simple inhomogenities with DSolve