Matt Parker has a nice video discussing the smallest prime p that satisfies Tan[p] > p, namely a user submitted 46 digit prime:

p == 1169809367327212570704813632106852886389036911

In the video he discusses why such primes are difficult to find and that no other such prime is known. It's worth a watch and can be seen here.

In this post we will find 3 new primes satisfying this inequality. These are large integers and are roughly

2.308358707825588 * 10^1016
4.094619989884699 * 10^35084
1.086855570320019 * 10^43176

We will assume an integer n being prime and satisfying Tan[n] > n are two independent conditions and both occurring simultaneously is effectively by chance. Therefore we can find a set of integers satisfying one condition and then filter with the other condition.

Now we know from the prime number theorem that for a given upper bound x there are about x/Log[x] primes.

Though sublinear, primes are much more frequent than the other condition Tan[n] > n. Consider the plot of Tan[x] and x, where the red regions represent the domain where such integers n can occur:

Plot[{Tan[x], x}, {x, 0, 9π}, 
  Filling -> {1 -> {2}}, FillingStyle -> {Opacity[0], Append[Red, 1]}, 
  PlotStyle -> Directive[Thin, Black], PlotRange -> {0, 9π}, AspectRatio -> 1/2]

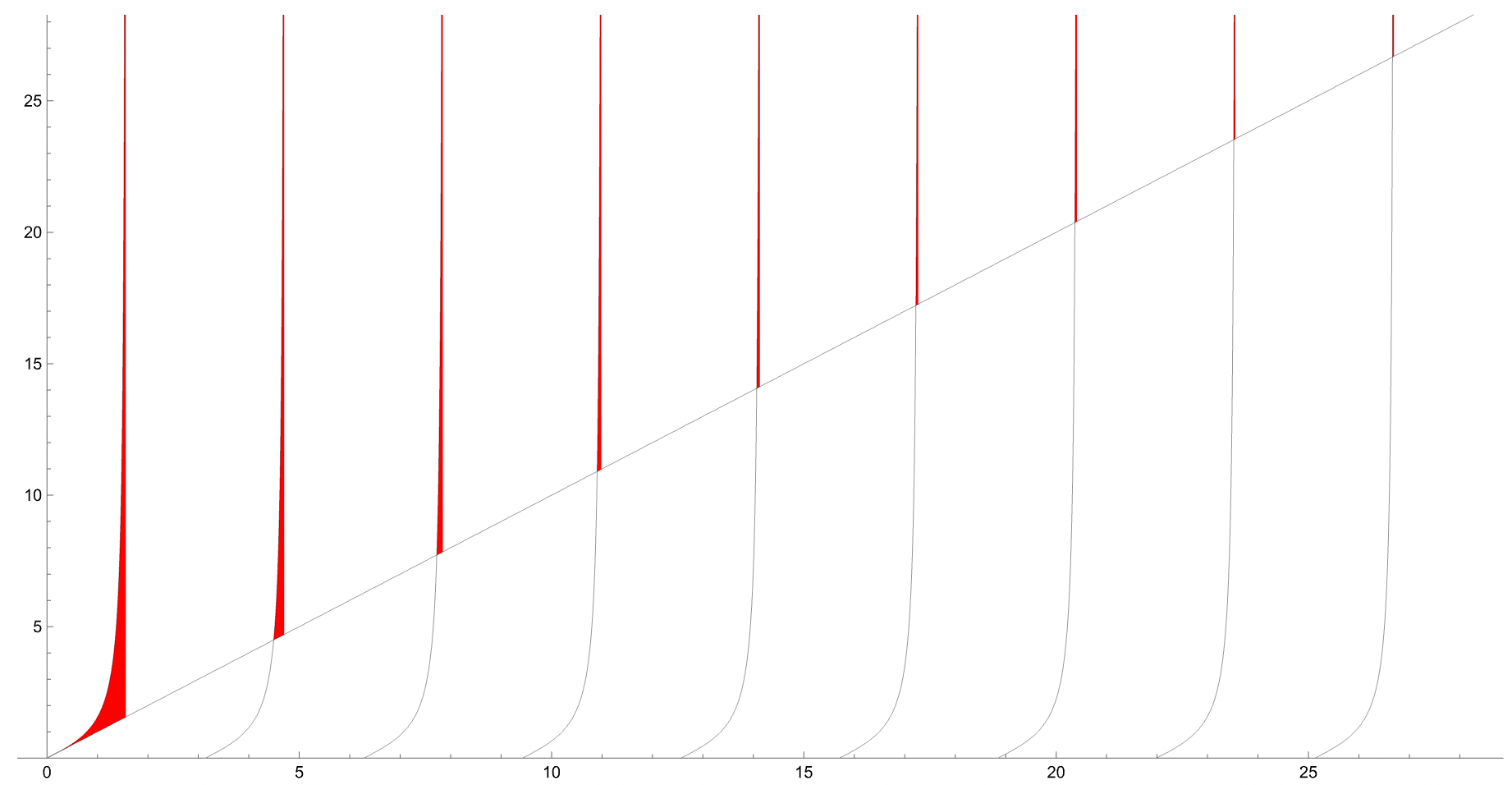
To look for the width of the regions we consider Tan[n π + π/2 - ε] == n π + π/2 - ε, where here ε is the width of the nth red region:

AsymptoticSolve[
 Normal @ Series[Refine[Tan[n π + π/2 - ε], n ∈ Integers], {ε, 0, 1}]] == n π + π/2 - ε,
 ε -> 0, n -> ∞, Reals
]
 (* {{ε -> 1/(n π)}} *)

Thus, summing the ε's that intersect (0, x) we expect roughly Log[x]/π integers n to satisfy Tan[n] > n.

Therefore our strategy is to find integers n that satisfy Tan[n] > n and then to check if they're also prime.

Method 1 Convergents

Since ε is far less than 1, we can get a bit fuzzy and look for n such that Tan[n] ≈ n. This means we're looking for integers n such that n ≈ k π + π/2 for some integer k. Isolating π, we can see this means we are looking for a tight rational approximation for π of the form

π ≈ (2n)/(2k+1)

Now, it's well known that convergents provide the best rational approximations (in a quantifiable sense) -- and so a heuristic is to find the convergents of π with an even numerator, then check if half that numerator satisfies our inequality:

Block[{$MaxExtraPrecision = ∞},
  Length[cands = Select[Select[Numerator[Convergents[π, 100000]], EvenQ]/2, Tan[#] > # &]]
]
 (* 16778 *)

We see here that of the first 100,000 convergents of π, roughly one sixth of them yield integers satisfying our inequality. And to get a sense of magnitude, this covers integers ranging up to ~10^51000:

N[Last[cands]]
 (* 2.129263410447718 * 10^51420 *)

Lastly we filter for the primes:

ppQ = ParallelMap[
   Block[{$MaxExtraPrecision = ∞}, 
     If[PrimeQ[#], Print[N[#]]; True, False]] &, cands, 
   ProgressReporting -> True, Method -> "ItemsPerEvaluation" -> 10];

Position[ppQ, True]
 (* {{13}, {314}, {11440}} *)

primes = Pick[cands, ppQ];

N[primes]
(* {1.16981 * 10^45, 2.308358707825588 * 10^1016, 4.094619989884699 * 10^35084} *)

So we found the same prime in Matt Parker's video plus two more!

Method 2 Lattice Reduction

Did we exhaustively search for all the primes less than 10^51000 above? Well, no -- we just employed a (powerful) heuristic. In fact based on the largest convergent we found, the number candidates, and the asymptotic formula for integers that satisfy our inequality, method 1 found about half of the candidates to filter from in its search domain.

A big sledge hammer in integer relation algorithms (but still a heuristic here) is that of lattice reduction.

Lattice reduction takes in a basis of integer vectors and returns a new integer basis spanning the same space, where each vector has a 'small' Euclidean norm. A simple application to find nontrivial relationships can be seen in the ref page for LatticeReduce here.

Similar to section 4.2 of my paper Computations of the Mertens Function and Improved Bounds on the Mertens Conjecture which looks for multiple simultaneous approximations for π, we can use LatticeReduce as follows for a single approximation to π:

TancN[ν_, base_:10] :=
  Block[{X, A, B, k, n, pQ, $MaxExtraPrecision = ∞},
    X = base^ν;
    A = {
      {Floor[π/2*X], base^10*X, 0},
      {Floor[π*X],   0,         1},
      {-X,           0,         0}
    };

    B = LatticeReduce[A];

    k = MaximalBy[B, Max[Abs[#]]&][[1, -1]];
    n = Abs[Round[π*k + π/2]];

    pQ = Tan[n] > n && PrimeQ[n];
    If[pQ, Print[{ν, N[n]}]];

    n -> pQ
  ]

And after about 8.5 hours of computing:

data = ParallelMap[TancN, Range[100000], ProgressReporting -> True]; // AbsoluteTiming

Length[primes = Union[Cases[data, (p_ -> True) :> p]]]
 (* 4 *)

The primes we get are the three from before plus a new one:

N[primes]
 (* {1.16981 * 10^45, 2.308358707825588 * 10^1016, 
   4.094619989884699 * 10^35084, 1.086855570320019 * 10^43176} *)

The Data

The full integer data for these primes can be downloaded here:

obj = CloudObject["https://www.wolframcloud.com/obj/0dec6477-4d21-49a6-8c14-eb8618af9917"];

The data:

primes = CloudGet[obj];

N[primes]
 (* {1.16981 * 10^45, 2.308358707825588 * 10^1016, 
   4.094619989884699 * 10^35084, 1.086855570320019 * 10^43176} *)