Thanks, Michael Rogers. As an unsophisticated user, I appreciate the examples and simplicity of your explanation. You even wrapped y > 0 in TrueQ[].

From your explanation, I expected continuous updating on the first example that iterates through Sin[] but did not see that. The cell bracket was not emphasized, and Windows Task Manager didn't show Mathematica doing much work.

I like your preferred method. I don’t have much need to set a global variable inside a Manipulate. If I needed a result outside the Manipulate, I would define the function there and invoke it inside the Manipulate.

I haven’t used With[] much, but from its documentation, it looks like Module[] accomplishes the same thing. I'm more familiar with Module[]. In fact, I didn’t immediately notice anything With[] does that Module[] doesn’t do. You helped me understand the difference between With[] and Assuming[] in an earlier thread.

If you would, I’d appreciate you expanding on the role of Dynamic[] in the last example. That might explain something that’s still not clear to me. Namely, how does activating the animation internal to Manipulate[] affect the things you said about avoiding unneeded updating.

Suppose we have a CompoundExpression[] consisting of a sequence of expressions a1[A]; b1[A,B], which we separate into two code blocks a1[A] and b1[A,B] with the following properties:

• a1[A] depends on only the variable A appears and not the variable B.
• b1[A, B] depends on the variable B and the variable A.

The dependency imagined is that the values computed in b1[A,B] depend on the values computed in a1[A], and the values in a1[A] need to be recomputed only if A changes. Thus if A changes, then both a1[A] and b1[A,B] need to be executed. If B changes, then only b1[A,B] needs to be executed.

Let's consider what happens when we wrap a code block in Dynamic[]. This does two things: It restructures the expression, and it changes how and when the block will be evaluated. The first is important for understanding the second. I may be biased by my upbringing to think in code blocks. It's better to think in terms of expression trees in WL, and the addition of Dynamic[] in a1[A]; Dynamic[b1[A,B]] creates a new subtree inside the outer CompoundExpression[].

In the problem at hand, the last Manipulate[]in my first post, the initialization code a1[A] is nested in With[] statements, rather than in a CompundExpression[]. This difference is not important to how the interior Dynamic[] functions. Note that when a Manipulate[body,...] is instantiated in the front end, the body is wrapped in Dynamic[]. So the question is about adding a Dynamic[] inside an outer Dynamic[].

Manipulate[
 With[{x = a^2},(* a1[A]; A=a *)
  Pause[1];  (* expensive step *)
  Dynamic[x + b] (* b1[A,B]; B=b *)
  ],
 {a, 0, 1}, {b, 0, 1}]

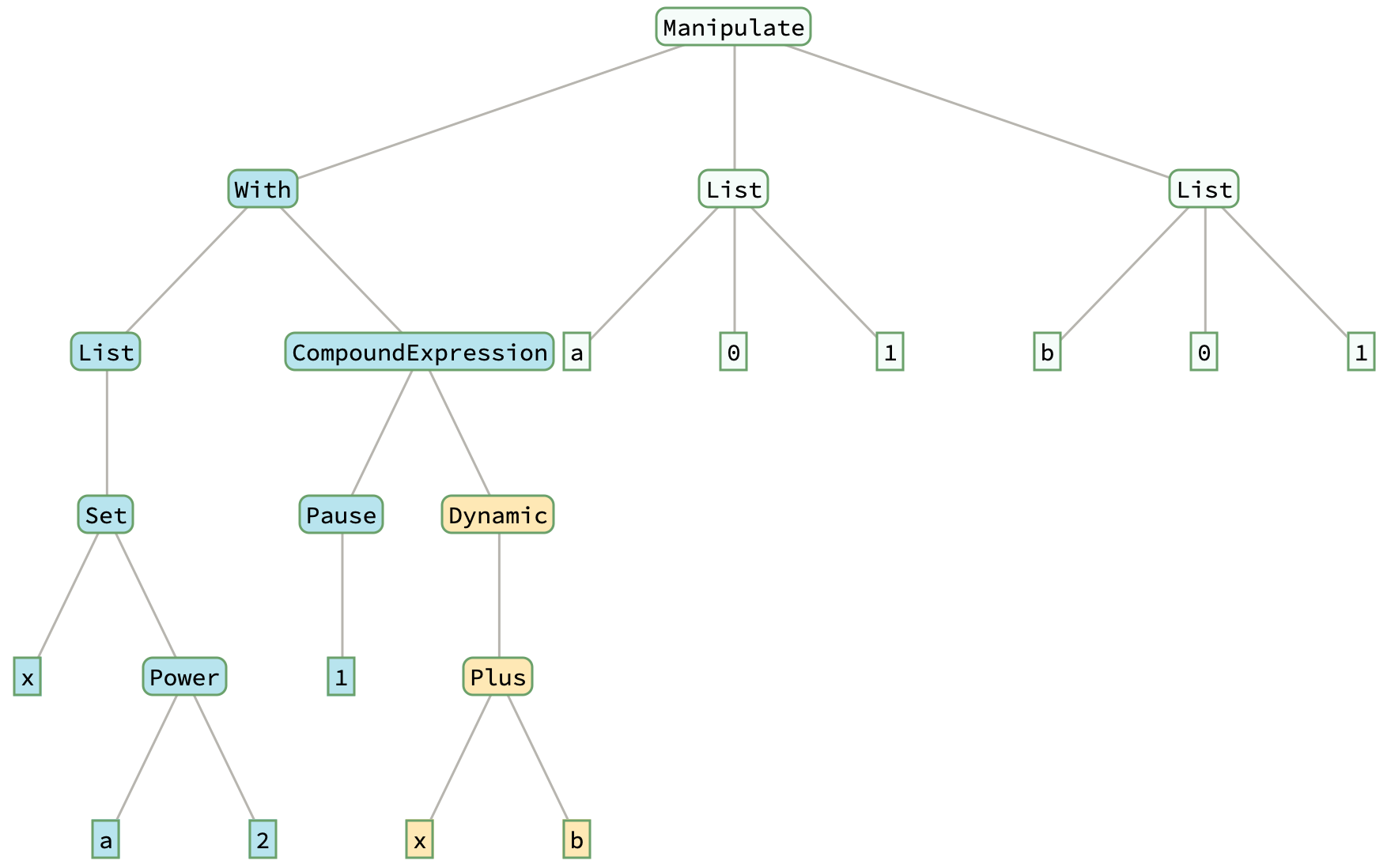
Wrapping code in Dynamic[] creates a subtree that may be reevaluated independently, when dynamic updating and dependencies allow it. Because Dynamic[] is HoldFirst, it prevents the code block from being evaluated immediately, about which I will say more in the paragraph following the next one.

For now, observe how the Manipulate[] example above behaves. It is expensive (time-wise) to update after changes in a, but inexpensive to update after changes in b. The extra Dynamic[] allows the part that depends on b (gold-ish subtree) to be updated independently of the part that depends only on a (blue-ish components). When a changes, the change causes the With subtree, comprising the blue and gold components, to be reevaluated; the new value substituted for x then triggers an update of the contents of the gold Dynamic[], and x+b is evaluated (and displayed).

Note that when Dynamic[expr] is "evaluated" -- specifically, when it is evaluated by the kernel -- essentially nothing happens. It evaluates to the expression Dynamic[expr]. The argument expr is not evaluated because Dynamic[] has the attribute HoldFirst and does not itself evaluate expr. The functionality of Dynamic[expr] comes about only when such a dynamic expression is displayed in a notebook. The front end is responsible for when to evaluate (or update) and display expr.

For instance, wrapping the both blocks in Dynamic[], as in Dynamic[a1[A]]; Dynamic[b1[A,B]], destroys the functionality, because in evaluating the expression, the Dynamic[a1[A]] is evaluated, which does nothing, then Dynamic[b1[A,B]] is evaluated, which does nothing but is the value of theCompoundExpression[]. The expression Dynamic[a1[A]] is forgotten; if the Dynamic[b1[A,B]] is displayed, the front end will evaluate b1[A,B]. Since a1[A] is never evaluated, b1[A,B] will be evaluated without the initialization performed by a1[A] ever being done.

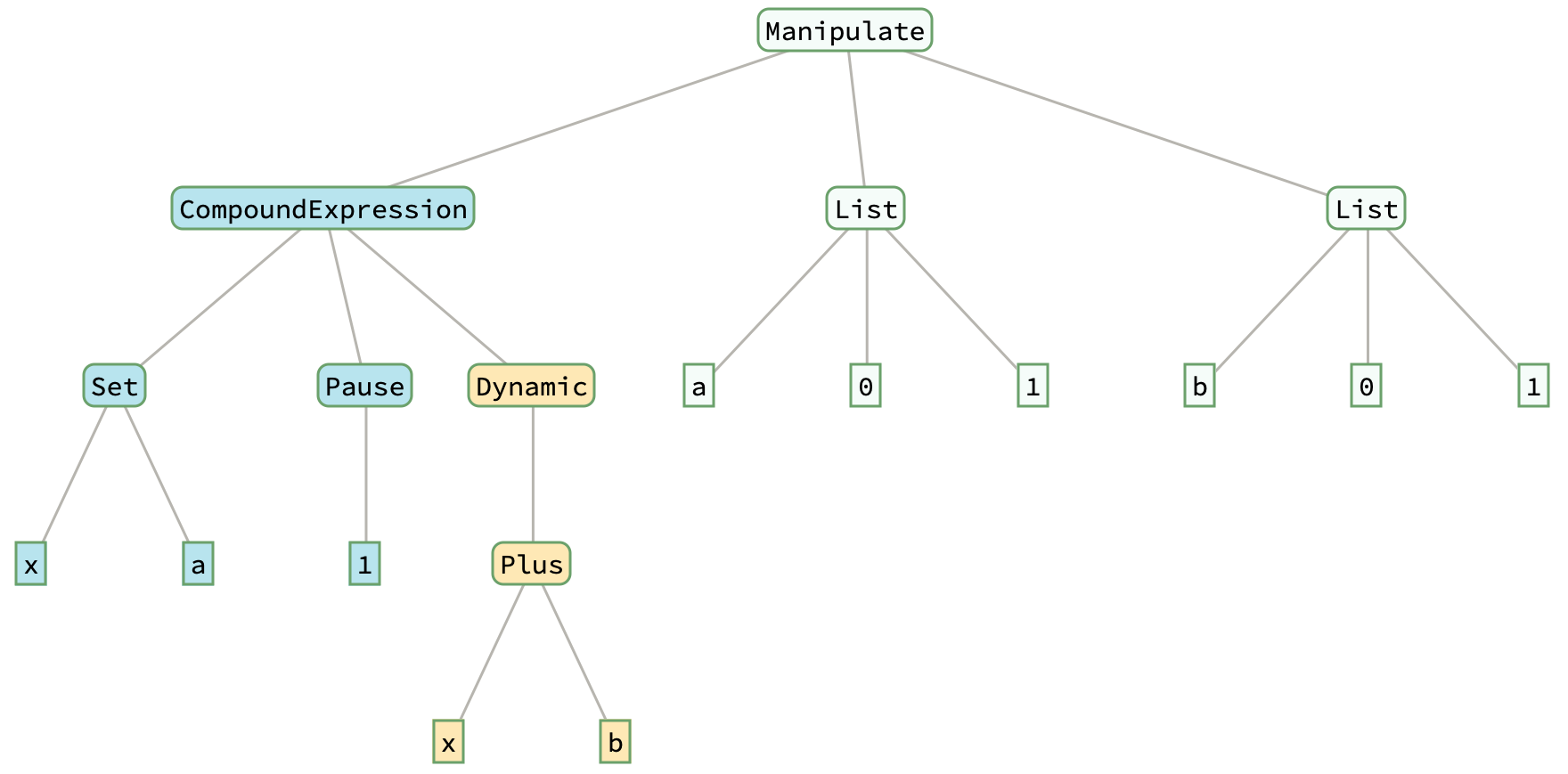
Clear[x];
Manipulate[ (* x is set when a changes *)
 x = a; Pause[1];(* a1[A]; A={a,x} *)
 Dynamic[x + b],(* b1[A,B]; B=b; x depends on A *)
 {a, 0, 1}, {b, 0, 1}]

Clear[y];
Manipulate[ (* y not set when a changes *)
 Dynamic[ (* a1[A] never evaluated, never displayed *)
  y = a; Pause[1]];
 Dynamic[y + b], (* Dynamic[b1[A,B]] is the value displayed *)
 {a, 0, 1}, {b, 0, 1}]

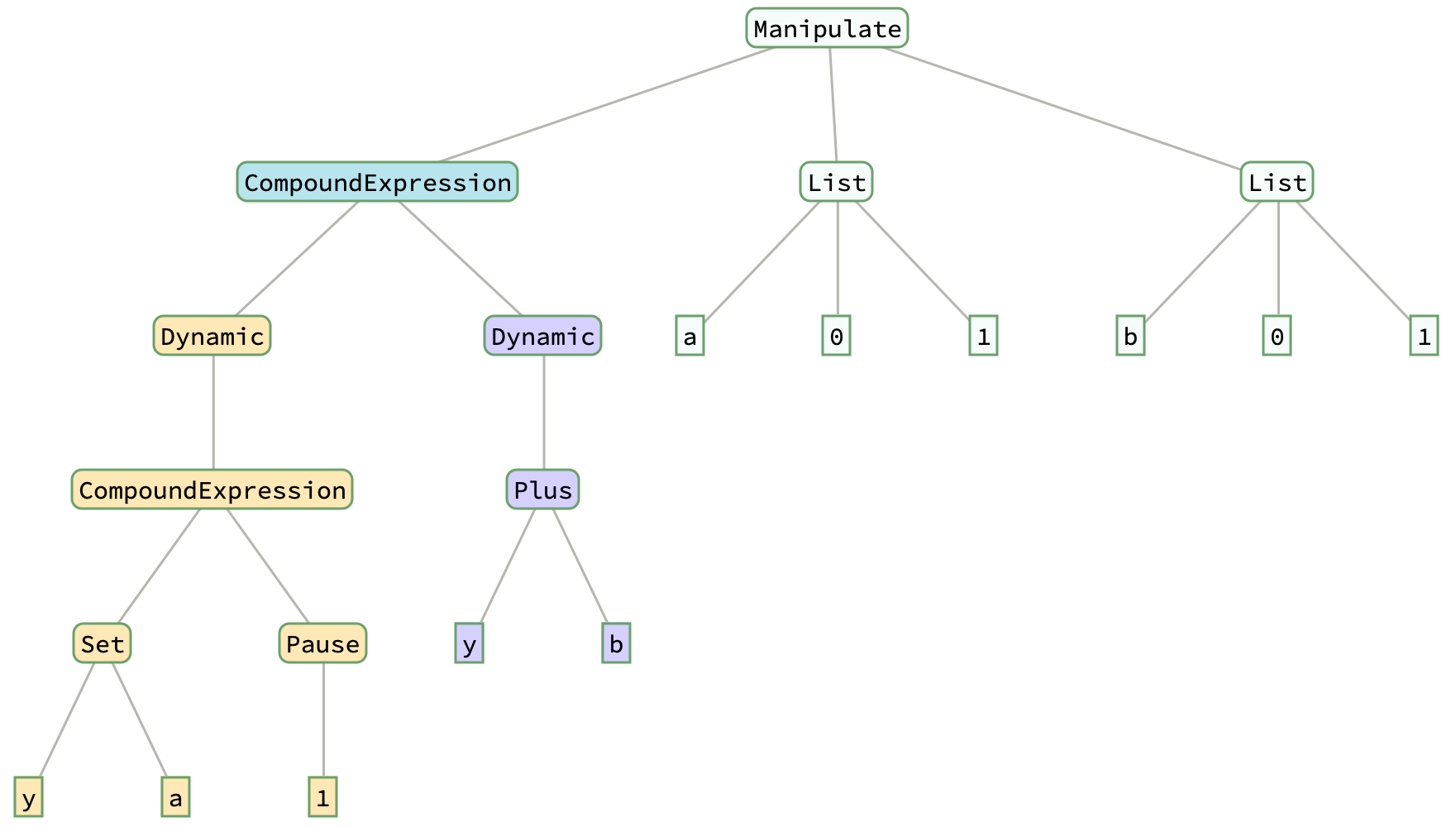
The left, gold subtree in the second "y" Manipulate[] has no effect on the operation of Manipulate[].

I don't know if that helps with your question about animation and unneeded updating, but I'll reiterate: If the unneeded updating takes a negligible amount of time, then it's probably best and simplest not to try to avoid it.