Suppose we have a CompoundExpression[] consisting of a sequence of expressions a1[A]; b1[A,B], which we separate into two code blocks a1[A] and b1[A,B] with the following properties:
a1[A] depends on only the variable A appears and not the variable B.b1[A, B] depends on the variable B and the variable A.
The dependency imagined is that the values computed in b1[A,B] depend on the values computed in a1[A], and the values in a1[A] need to be recomputed only if A changes. Thus if A changes, then both a1[A] and b1[A,B] need to be executed. If B changes, then only b1[A,B] needs to be executed.
Let's consider what happens when we wrap a code block in Dynamic[]. This does two things: It restructures the expression, and it changes how and when the block will be evaluated. The first is important for understanding the second. I may be biased by my upbringing to think in code blocks. It's better to think in terms of expression trees in WL, and the addition of Dynamic[] in a1[A]; Dynamic[b1[A,B]] creates a new subtree inside the outer CompoundExpression[].
In the problem at hand, the last Manipulate[]in my first post, the initialization code a1[A] is nested in With[] statements, rather than in a CompundExpression[]. This difference is not important to how the interior Dynamic[] functions. Note that when a Manipulate[body,...] is instantiated in the front end, the body is wrapped in Dynamic[]. So the question is about adding a Dynamic[] inside an outer Dynamic[].
Manipulate[
With[{x = a^2},(* a1[A]; A=a *)
Pause[1]; (* expensive step *)
Dynamic[x + b] (* b1[A,B]; B=b *)
],
{a, 0, 1}, {b, 0, 1}]
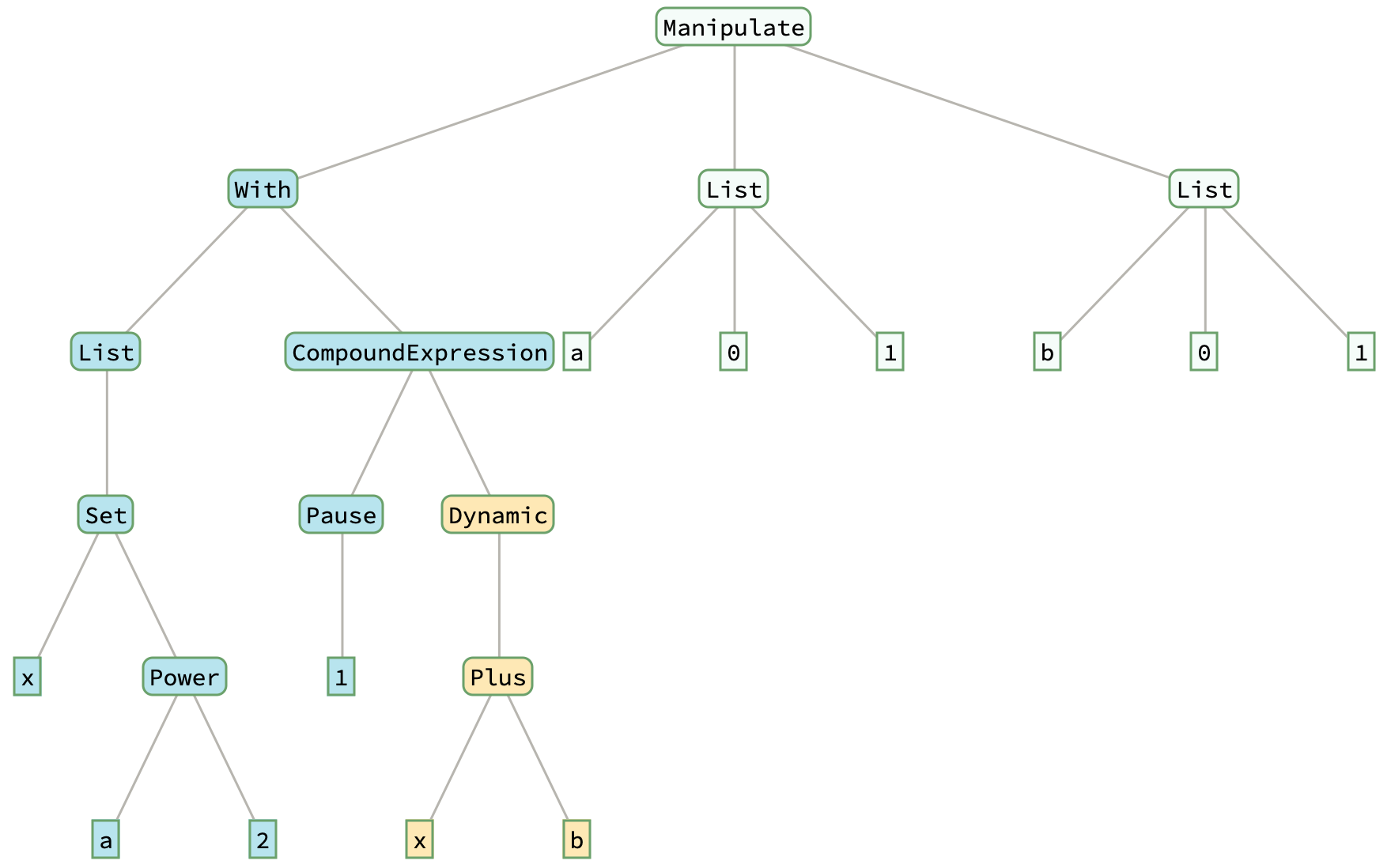
Wrapping code in Dynamic[] creates a subtree that may be reevaluated independently, when dynamic updating and dependencies allow it. Because Dynamic[] is HoldFirst, it prevents the code block from being evaluated immediately, about which I will say more in the paragraph following the next one.
For now, observe how the Manipulate[] example above behaves. It is expensive (time-wise) to update after changes in a, but inexpensive to update after changes in b. The extra Dynamic[] allows the part that depends on b (gold-ish subtree) to be updated independently of the part that depends only on a (blue-ish components). When a changes, the change causes the With subtree, comprising the blue and gold components, to be reevaluated; the new value substituted for x then triggers an update of the contents of the gold Dynamic[], and x+b is evaluated (and displayed).
Note that when Dynamic[expr] is "evaluated" -- specifically, when it is evaluated by the kernel -- essentially nothing happens. It evaluates to the expression Dynamic[expr]. The argument expr is not evaluated because Dynamic[] has the attribute HoldFirst and does not itself evaluate expr. The functionality of Dynamic[expr] comes about only when such a dynamic expression is displayed in a notebook. The front end is responsible for when to evaluate (or update) and display expr.
For instance, wrapping the both blocks in Dynamic[], as in Dynamic[a1[A]]; Dynamic[b1[A,B]], destroys the functionality, because in evaluating the expression, the Dynamic[a1[A]] is evaluated, which does nothing, then Dynamic[b1[A,B]] is evaluated, which does nothing but is the value of theCompoundExpression[]. The expression Dynamic[a1[A]] is forgotten; if the Dynamic[b1[A,B]] is displayed, the front end will evaluate b1[A,B]. Since a1[A] is never evaluated, b1[A,B] will be evaluated without the initialization performed by a1[A] ever being done.
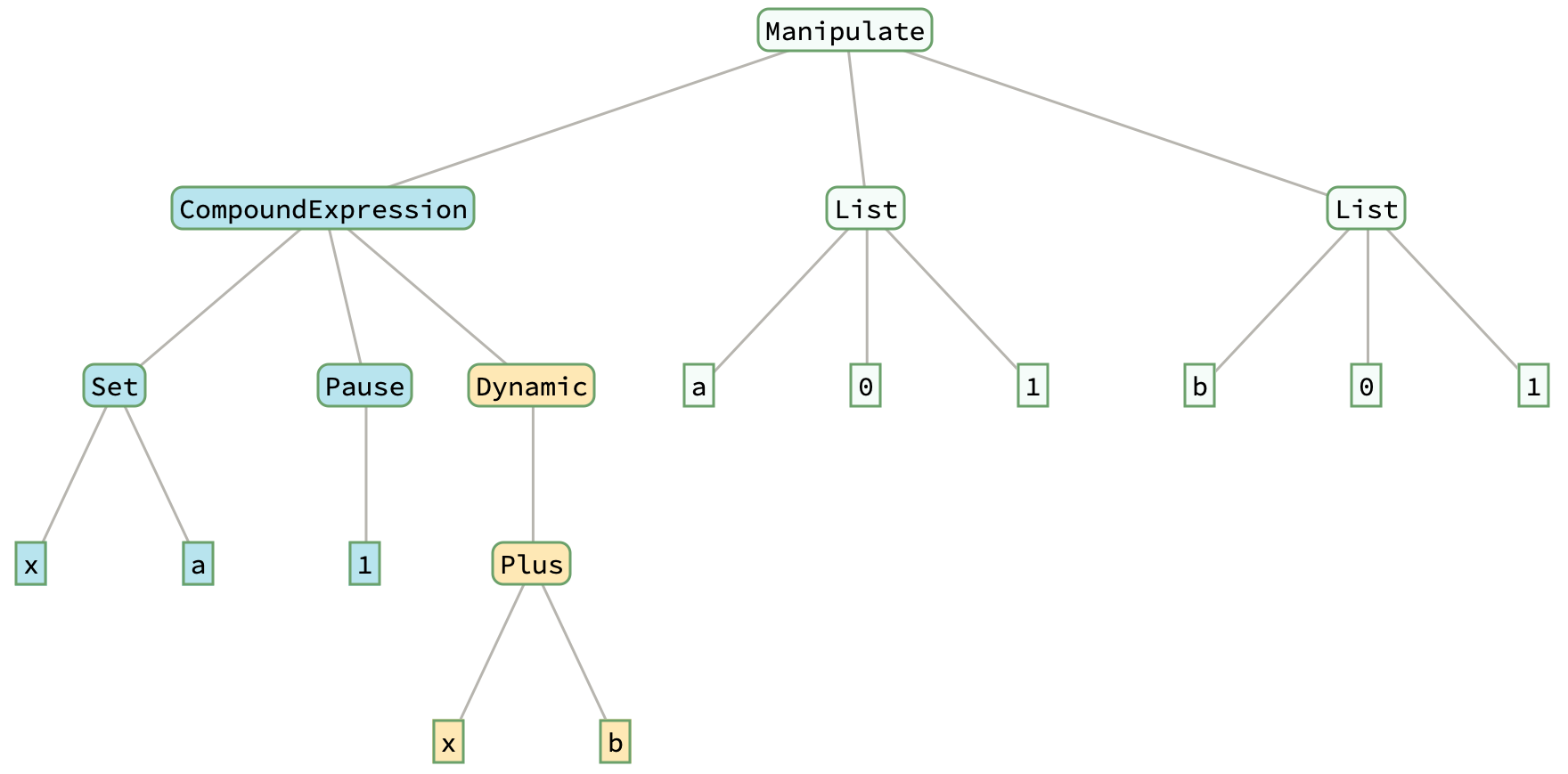
Clear[x];
Manipulate[ (* x is set when a changes *)
x = a; Pause[1];(* a1[A]; A={a,x} *)
Dynamic[x + b],(* b1[A,B]; B=b; x depends on A *)
{a, 0, 1}, {b, 0, 1}]
Clear[y];
Manipulate[ (* y not set when a changes *)
Dynamic[ (* a1[A] never evaluated, never displayed *)
y = a; Pause[1]];
Dynamic[y + b], (* Dynamic[b1[A,B]] is the value displayed *)
{a, 0, 1}, {b, 0, 1}]
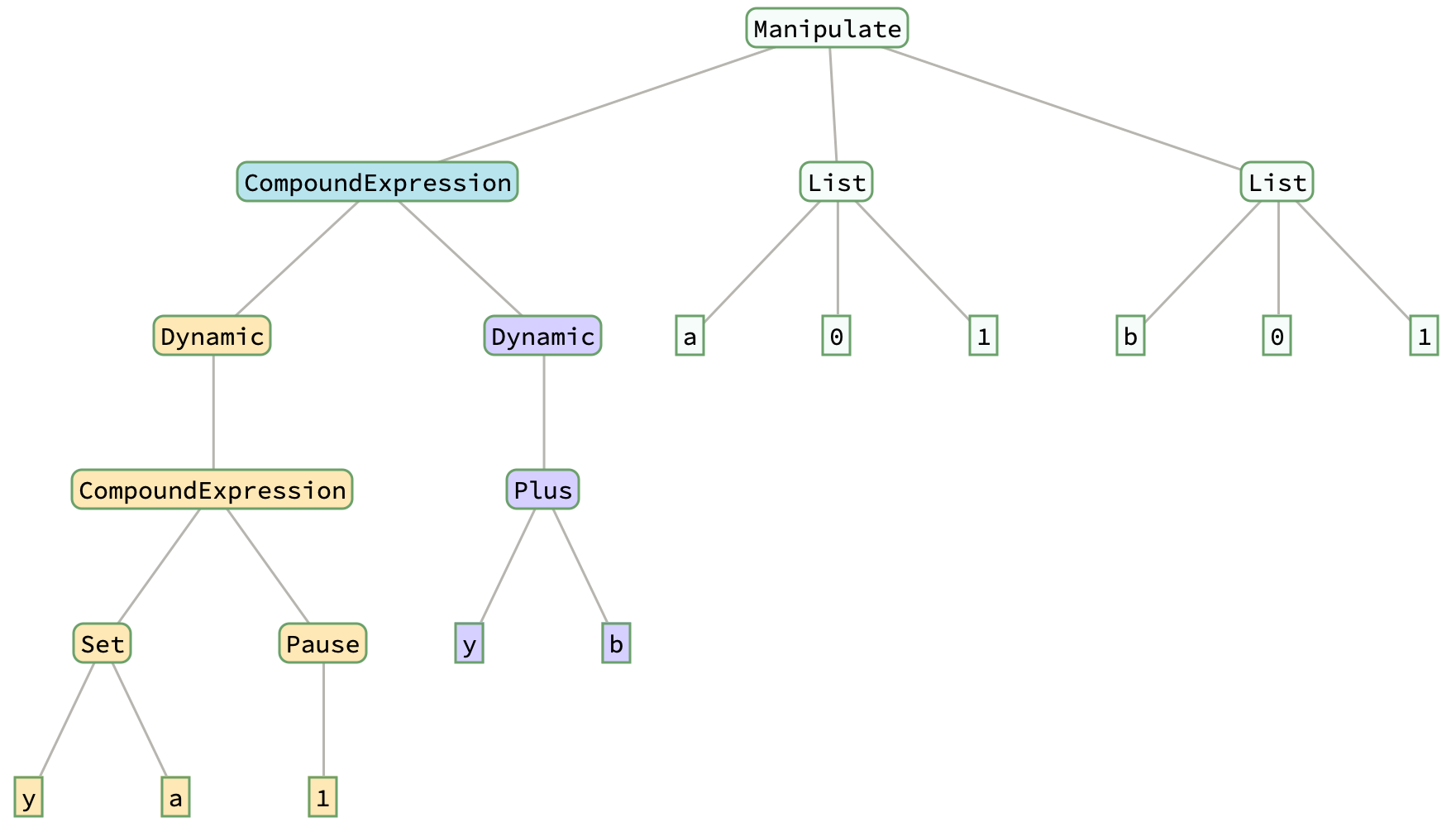
The left, gold subtree in the second "y" Manipulate[] has no effect on the operation of Manipulate[].
I don't know if that helps with your question about animation and unneeded updating, but I'll reiterate: If the unneeded updating takes a negligible amount of time, then it's probably best and simplest not to try to avoid it.