Perhaps you are to turn it into a continuous problem, rather than discrete. The code below writes the relationship as coupled diffeqs and solves the system for general initial conditions. We find that Twitter will enjoy 60% of the market. When you apply the evolution rule to these numbers, you find that for the discrete system it is in steady state.

In[1]:= eqs = {
   fb'[d] == -0.3 fb[d] + 0.2 tw[d],
   tw'[d] == 0.3 fb[d] - 0.2 tw[d],
   fb[0] == fb0, tw[0] == tw0
   };

In[2]:= sol = DSolve[eqs, {fb[d], tw[d]}, d][[1]];

In[3]:= Limit[{fb[d], tw[d]} /. sol, d -> Infinity]

Out[3]= {0.4 (1. fb0 + 1. tw0), 0.6 (1. fb0 + 1. tw0)}

Hi,

I am not sure whether I typed something in wrong, but you could try this. Suppose that you write a vector, the first component of which is the percentage of Facebook users and the second the percentage of Twitter users. The process is Markovian. These transition matrices (or probability matrices) have the characteristic that the columns add up to one. In your case the matrix is

matrix = {{0.7, 0.2}, {0.3, 0.8}}

If you use

MatrixForm[matrix]

it looks more familiar.

Okay. After one step the things looks like this

matrix.{0.6, 0.4}

i.e. you multiply the matrix with the vector. You can use NestList to iterate that:

NestList[matrix.# &, matrix, 20].{0.6, 0.4}

The result of this is

{{0.5, 0.5}, {0.45, 0.55}, {0.425, 0.575}, {0.4125, 0.5875}, {0.40625,
   0.59375}, {0.403125, 0.596875}, {0.401563, 0.598438}, {0.400781, 
  0.599219}, {0.400391, 0.599609}, {0.400195, 0.599805}, {0.400098, 
  0.599902}, {0.400049, 0.599951}, {0.400024, 0.599976}, {0.400012, 
  0.599988}, {0.400006, 0.599994}, {0.400003, 0.599997}, {0.400002, 
  0.599998}, {0.400001, 0.599999}, {0.4, 0.6}, {0.4, 0.6}, {0.4, 0.6}}

This shows you that it settles down to a ratio of 40% Facebook vs 60% Twitter. you can also plot the process:

ListPlot[Transpose[NestList[matrix.# &, matrix, 20].{0.6, 0.4}]]

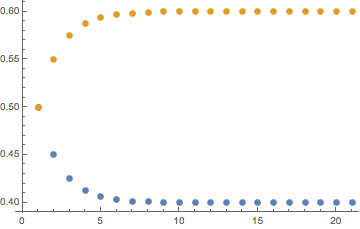
Of course this is not really a water-tight argument. There is however a theorem that helps. On page 107 of "A Course on the Web Graph" you find an argument that shows that the dominant eigenvector, i.e. the one with eigenvalue 1, gives under some conditions the final ratio. In Mathematica the eigenvectors are ordered with respect to their eigenvalues so

Eigenvectors[matrix][1]

gives the correct ratio of

{-0.5547, -0.83205}

Note that the negative of this is also an eigenvector. Also we can normalise it to one, i.e. 100%, like so:

 Eigenvectors[matrix][[1]]/Total[ Eigenvectors[matrix][[1]]]

which gives:

{0.4, 0.6}

So if I haven't made some stupid typo, the ratio of Facebook/Twitter followers will invert the original ratio in the example you gave.

Hope this helps, Marco

PS: I am aware that this does not really add much to what Daniel already said, but I had already started typing...

It involves linear algebra, or at least can be set up that way. A certain 2x2 matrix gives the transitions from one day to another. So multiplying that matrix by today's preference fraction vector of {.6,.4} will give tomorrow's preferences. Multiply again to get the prefs for the day after. Etc.

Some experimenting might give an idea of whether this stabilizes. If you have covered matrix powers, that could also be quite useful here.

This can also be set up as a recurrence problem (which, under the hood, will use similar technology to the linear algebra approach). If we denote days by n then one equation might be f[n+1]==7/10*f[n]+1/5*t[n]. For solving recurrences in Mathematica there is RSolve.