When a lengthy math expression is to be evaluated on a pocket calculator(-app) usually the algebraic notation is used - i.e the expression is keyed in simply "as it is", using parenthesis, etc.. But there is another notation (notably RPN) which is by far superior because the expression is keyed in in a much more mathematical way.
Its advantages are e.g.: Less keystrokes, no parenthesis, less error-prone. The only disadvantage is: One needs a tiny amount of effort getting used to it. (This was enough of not becoming the widespread and popular notation - what does that say about mankind?)

Luckily there are still RPN-calculators available - and not just apps/programs (e.g. dc or Free42) but also real (and excellent!) hardware (e.g. SwissMicros).

Due to the mathematical way of RPN on one hand and WL on the other it is surprisingly easy to convert an expression from Mathematica to RPN. Just by looking at expressions using Treeform[] or ExpressionGraph[] one can get a reasonable suspicion for this:

(* example - lengthy expression: *)
expr = D[Log[x^2 y] Exp[x Sin[x^2 Sqrt[a x y]]], {x, 1}] // FullSimplify

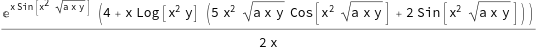
(* some cosmetics: *)
exprRPN = 
  expr //. {Plus -> "+", 
     Times[-1, a_] :> "+\[NegativeThinSpace]/\[NegativeThinSpace]-"[a],
      Times -> "*", Power[a_, Rational[1, 2]] :> "\!\(\*SqrtBox[\(\\\\ \\\\ \)]\)"[a],
      Power[E, exp_] :> "e^"[exp], Power[a_, b_] :> ("\[Wedge]"[b, a]),
      Rational[1, a_] :> (1./a)} //. {op_[a_, b_, c_, d__] :> op[op[a, b], op[c, d]], op_[a_, b_, c_] :> op[op[a, b], c]};

vsf[{xc_, yc_}, name_, {w_, h_}] :=
  Block[{xmin = xc - 2 w, xmax = xc + 2 w, ymin = yc - h, 
    ymax = yc + h}, {Opacity[.1], Polygon[{{xmin, ymin}, {xmin, ymax}, {xmax, ymax}, {xmax, ymin}}]}
   ];
ExpressionGraph[exprRPN, GraphLayout -> "LayeredDigraphEmbedding", 
 EdgeShapeFunction -> ({Gray, Arrowheads[.02], Arrow[Reverse@#, .3]} &),
 VertexLabels -> Placed[Automatic, Center], VertexSize -> .4, VertexLabelStyle -> Directive[Red, 20],
 VertexShapeFunction -> vsf, ImageSize -> 800]

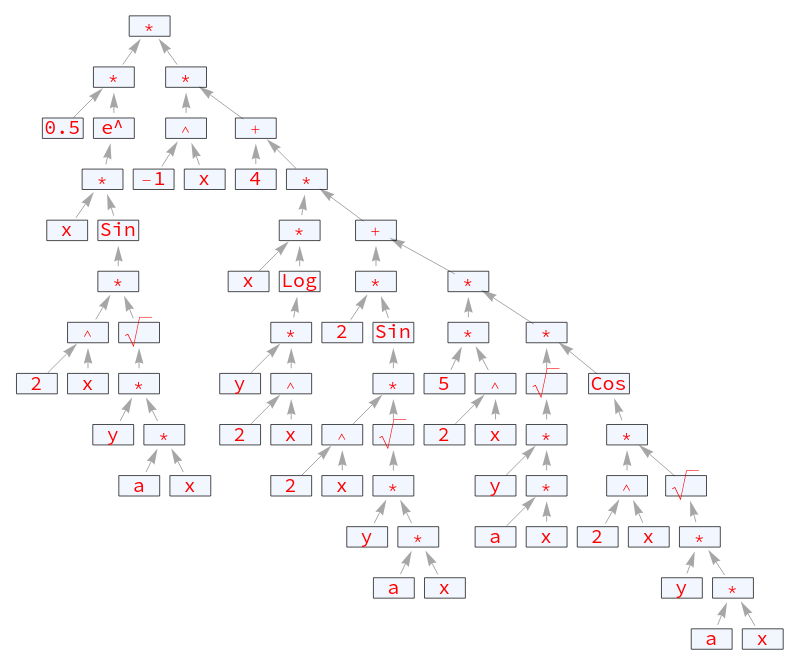
Basically in the above one had to make sure that operators like Plus[] and Times[] do not get more than two operands at a time, everything else is just "cosmetics".

The substantial command for the conversion in general now simply is: Reverse@Level[<expr>, {-1}, Heads -> True]

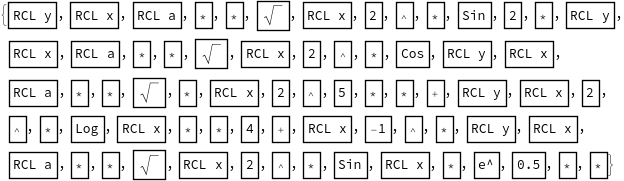
Finally one gets the necessary keystrokes:

symbolRules = Rule[#, "RCL " ~~ ToString[#]] & /@ DeleteDuplicates[Cases[exprRPN, _Symbol, All]];
operationSequence = Framed /@ (Reverse@Level[exprRPN, {-1}, Heads -> True] /. symbolRules)

Of course those results can be used for creating an executable for the respective calculator, but my goal here was just a "proof of concept".