I am interested in Fomes Fomentarius or "Tinder Polypore" mushroom patterns
(original photo, diagrams of Voronoi and Delaunay):

At first it seems something simple, like a sunflower seed pattern or even just a dense package. But the analysis shows that it is not so simple. In this post I found a connection between these patterns and the Poisson disk and Lloyd relaxation processes.
But this is only a descriptive side; the results of the generation are clearly more artificial than the natural picture.
I was told that these could be Turing patterns, which often appear in natural phenomena. In this article I found a relatively simple PDE system that generates something very similar:


It’s easy to implement this in Mathematica:
Clear[u, v, t, x, y, eqs, bndConds, sol, initConds, du, dv, f, k];
f = 0.039; k = 0.065; size = 1;
du = 0.00002; dv = 0.00001;
eqs = {D[u[t, x, y], t] ==
du Laplacian[u[t, x, y], {x, y}] - u[t, x, y]* v[t, x, y]^2 +
f (1 - u[t, x, y]),
D[v[t, x, y], t] ==
dv Laplacian[v[t, x, y], {x, y}] +
u[t, x, y] *v[t, x, y]^2 - (f + k) v[t, x, y]};
bndConds = {u[t, 0., y] == u[t, size, y], u[t, x, 0.] == u[t, x, size],
v[t, 0., y] == v[t, size, y], v[t, x, 0.] == v[t, x, size]};
initReg = 0.4 < x < 0.6 && 0.4 < y < 0.6;
initConds = {u[0., x, y] ==
Piecewise[{{0.5 + 0.01 Sin[20 x] Cos[20 y], initReg}}, 1.],
v[0., x, y] ==
Piecewise[{{0.25 + 0.01 Sin[20 y] Cos[20 x], initReg}}, 0.]};
sol = NDSolve[
Join[eqs, bndConds, initConds],
{u, v}, {t, 0, 15000}, {x, 0., size}, {y, 0., size}]
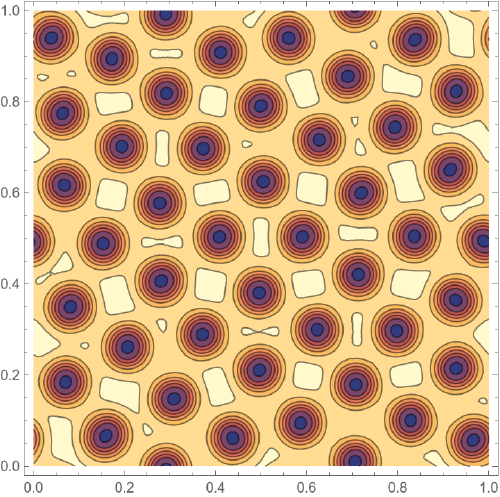
Question 1.
I’m not very good at PDE solving and use default settings.
But Mathematica’s capabilities in this area are quite large.
I really hope someone will figure out this simple system (ready to answer additional questions!) and find a way to optimize code. As you can see, my goal is to get the general pattern. Maybe it is worth to set a more rough step? The shown result comes at $t = 15000$, I would like faster.
Would like to get as many pores as possible.
But when I try to increase the size of the area size, the system gives a zero solution(
Question 2.
Intuitively I am sure that such pattern can be obtained not through PDE, but through cellular automata.
The simplest form of Game of Life with rule B0S345 gives an interesting (but not the right way) result:

Is there any way to create a two-layer cellular automata on the Wolfram Language, based on this system? Maybe someone else will come up with CA ideas that generate something like this.