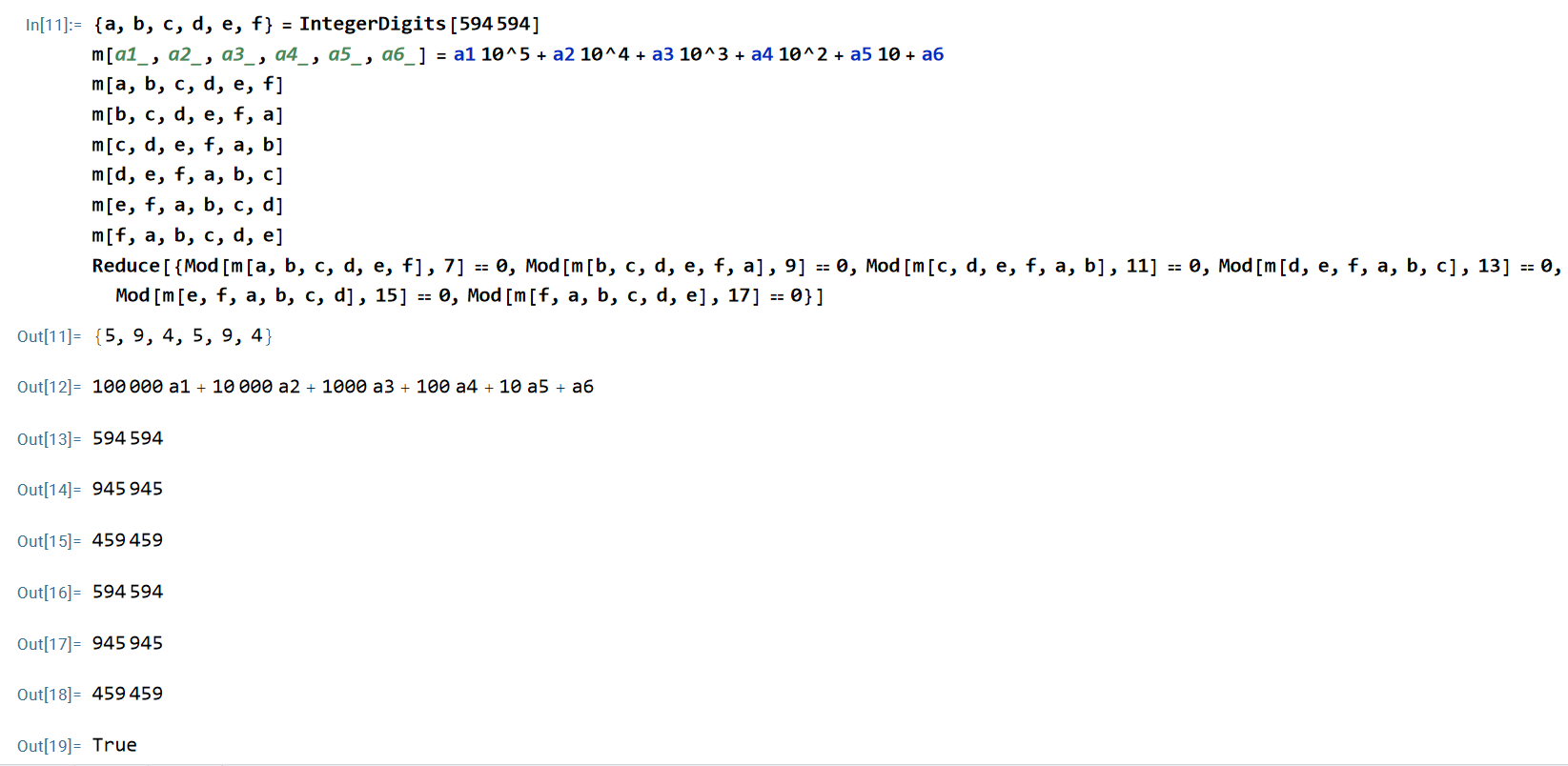
Knowing the answer in advance, the verification using the previous code is correct. However, I still don't know how to find this six-digit number.
{a = 5, b = 3, c = 1, d = 5, e = 3, f = 1}
m[a1_, a2_, a3_, a4_, a5_, a6_] =
a1 10^5 + a2 10^4 + a3 10^3 + a4 10^2 + a5 10 + a6
m[a, b, c, d, e, f]
m[b, c, d, e, f, a]
m[c, d, e, f, a, b]
m[d, e, f, a, b, c]
m[e, f, a, b, c, d]
m[f, a, b, c, d, e]
Reduce[{Mod[m[a, b, c, d, e, f], 7] == 0,
Mod[m[b, c, d, e, f, a], 9] == 0, Mod[m[c, d, e, f, a, b], 11] == 0,
Mod[m[d, e, f, a, b, c], 13] == 0,
Mod[m[e, f, a, b, c, d], 15] == 0,
Mod[m[f, a, b, c, d, e], 17] == 0}]

And
{a, b, c, d, e, f} = IntegerDigits[594594]
m[a1_, a2_, a3_, a4_, a5_, a6_] =
a1 10^5 + a2 10^4 + a3 10^3 + a4 10^2 + a5 10 + a6
m[a, b, c, d, e, f]
m[b, c, d, e, f, a]
m[c, d, e, f, a, b]
m[d, e, f, a, b, c]
m[e, f, a, b, c, d]
m[f, a, b, c, d, e]
Reduce[{Mod[m[a, b, c, d, e, f], 7] == 0,
Mod[m[b, c, d, e, f, a], 9] == 0, Mod[m[c, d, e, f, a, b], 11] == 0,
Mod[m[d, e, f, a, b, c], 13] == 0,
Mod[m[e, f, a, b, c, d], 15] == 0,
Mod[m[f, a, b, c, d, e], 17] == 0}]