Our collaborative effort to deconstruct the foundational principles of Ethernet has proven highly effective. By assembling and analyzing seminal documents on bandwidth and reliability, we are distilling a clear and compelling narrative for our work. The models currently in development directly address the central "knife edge" argument in modern networking: the tension between legacy protocols and the stringent demands of truly resilient distributed systems.

This tension is often masked by cultural inertia, such as the predisposition to model all network traffic, including unreliable flows, over TCP. Our work confronts this directly. The process of configuring the DÆDÆLUS Emulator to reflect our principles—versus configuring the physical Mac Mini Network—is itself an exercise in this contrast, highlighting the shift from legacy constraints to a new, physically-grounded computational model.

Our methodology is analogous to applying multiscale field theory to network flows. It is deeply informed by foundational papers like Reliable Full-Duplex File Transmission over Half-Duplex Telephone Lines and A Note on Reliable Full-Duplex Transmission over Half-Duplex Links. Furthermore, our public lectures on the "God's Eye View" of networks provide corroborating context for our models, challenging long-held but "untrue" assumptions, such as the notion that clocks can be perfectly synchronized across a distributed system. This work is a direct extension of the seminal concepts set forth in our initial research, serving as a record of the who, what, where, when, why, and how of our approach.

Redefining the Causal Link

At the core of our philosophy is a redefinition of the most basic network primitive. A causal link is not an irreversible fact asserted into a global matrix; it is a stateful, symmetric, and reversible interaction between two CELLs.

The Role of the Graph Virtual Machine (GVM)

Consequently, when a subtransaction is reversible, the GVM does not simply compute a static dependency graph. It actively manages a living, stateful fabric where causal links can be established, torn down, and deterministically rolled back. This approach allows the system to heal from faults and adapt to changing conditions using only local information. The result is a fabric that is fundamentally resilient to the failures and ambiguities of the physical world.

ClearAll["Global`*"];
idle=".";
sentinel="$";
states=Association["G"->"G","L"->"L","R"->"R","A"->"A","B"->"B","C"->"C","a"->"a","b"->"b","c"->"c","bB"->"bB","cC"->"cC","RL"->"RL","LR"->"LR","F"->"F","I"->idle];
stateColor=Association[idle->LightGray,"G"->Red,"L"->RGBColor[1,.6,.1],"R"->RGBColor[1,.6,.1],"A"->LightBlue,"B"->LightBlue,"C"->Blue,"a"->RGBColor[.65,.9,.65],"b"->RGBColor[.55,.8,.55],"c"->RGBColor[.45,.7,.45],"bB"->Purple,"cC"->Magenta,"RL"->Brown,"LR"->Yellow,"F"->Black];
leftChar[l_String]:=If[l===sentinel,sentinel,StringTake[l,-1]];
rightChar[r_String]:=If[r===sentinel,sentinel,StringTake[r,1]];
drawFrame[seq_List]:=Graphics[Table[{EdgeForm[GrayLevel[.3]],stateColor[seq[[i]]],Rectangle[{i-1,0},{i,1}],Inset[Style[seq[[i]],12,If[stateColor[seq[[i]]]===LightGray,Black,White],Bold],{i-.5,.5}]},{i,Length[seq]}],PlotRangePadding->None,ImageSize->Scaled[1],Background->White];
nextState[l_String,s_String,r_String]:=Module[{lLast=leftChar[l],rFirst=rightChar[r],join=l<>r},Which[s=="A",If[rFirst=="L","G","B"],s=="B","C",s=="C",If[rFirst=="L","G",idle],s=="a",If[lLast=="R","G","b"],s=="b","c",s=="c",If[lLast=="R","G",idle],s=="bB","cC",s=="cC",If[lLast=="R"||rFirst=="L","G",idle],s=="G",Which[MemberQ[{"$$","$G","G$","GG"},join],"F",r==idle&&l==idle,"bB",r==idle,"B",l==idle,"b",True,"G"],s=="L",Which[l==sentinel||lLast=="R","R",lLast=="C","G",r=="G","L",True,idle],s=="R",Which[r==sentinel||rFirst=="L","L",rFirst=="c","G",True,idle],s=="LR",If[lLast=="C"||rFirst=="c","G",idle],s=="RL","LR",s==idle,Which[(l=="G"||lLast=="R")&&(r=="G"||rFirst=="L"),"RL",l=="G"||lLast=="R","R",r=="G"||rFirst=="L","L",lLast=="C","A",rFirst=="c","a",True,idle],True,s]];
spaceTimeDiagram[rows_List]:=Module[{codes,crules},codes=Association[idle->0,"G"->1,"L"->2,"R"->3,"A"->4,"B"->5,"C"->6,"a"->7,"b"->8,"c"->9,"bB"->10,"cC"->11,"RL"->12,"LR"->13,"F"->14];crules={0->LightGray,1->Red,2->RGBColor[1,.6,.1],3->RGBColor[1,.6,.1],4->LightBlue,5->LightBlue,6->Blue,7->RGBColor[.65,.9,.65],8->RGBColor[.55,.8,.55],9->RGBColor[.45,.7,.45],10->Purple,11->Magenta,12->Brown,13->Yellow,14->Black};ArrayPlot[Reverse[rows/. codes],ColorRules->crules,Frame->False,AspectRatio->Automatic,ImageSize->Medium,PlotLabel->Style["Firing-Squad Synchronisation ("<>ToString[Length[rows]-1]<>" steps)",14,Bold]]];
animateEvolution[rows_List]:=ListAnimate[drawFrame/@rows,ImageSize->Scaled[1],DefaultDuration->6,AnimationRunning->False,AnimationRepetitions->1,ControlPlacement->Top];
updateSeq[seq_List]:=Module[{n=Length[seq]},Table[With[{l=If[i==1,sentinel,seq[[i-1]]],s=seq[[i]],r=If[i==n,sentinel,seq[[i+1]]]},nextState[l,s,r]],{i,n}]];
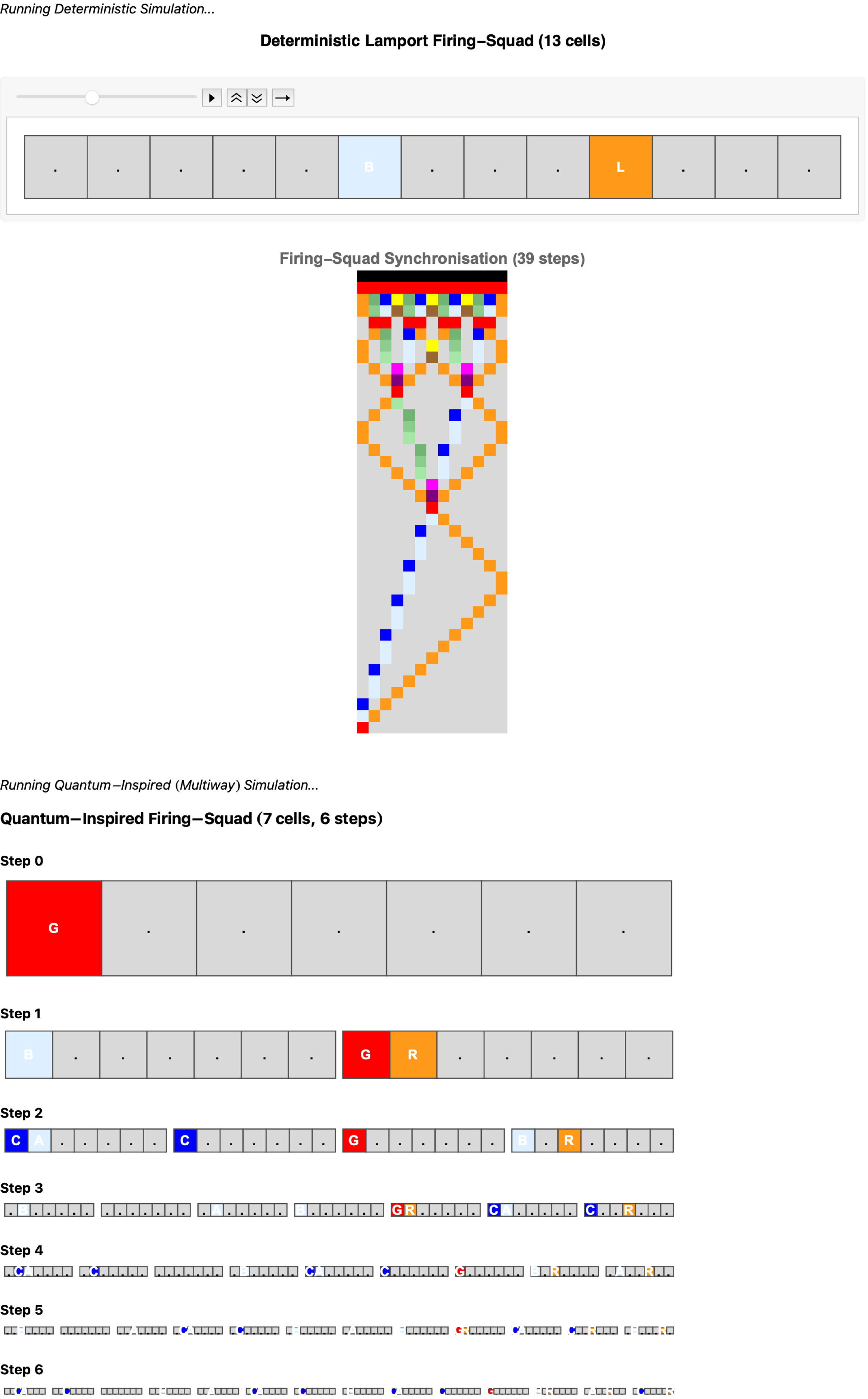
evolveDeterministicFSSP[n_Integer?Positive]:=Module[{seq,rows={}},seq=ConstantArray[idle,n];seq[[1]]="G";AppendTo[rows,seq];While[Union[seq]=!={"F"},seq=updateSeq[seq];AppendTo[rows,seq];];Column[{Style["Deterministic Lamport Firing-Squad ("<>ToString[n]<>" cells)",14,Bold],animateEvolution[rows],spaceTimeDiagram[rows]},Spacings->2,Alignment->Center,BaseStyle->{FontFamily->"Helvetica"}]];
updateSeqLR[seq_List]:=Module[{new=seq,n=Length[seq]},Do[new[[i]]=nextState[If[i==1,sentinel,new[[i-1]]],seq[[i]],If[i==n,sentinel,seq[[i+1]]]],{i,1,n}];new];
updateSeqRL[seq_List]:=Module[{new=seq,n=Length[seq]},Do[new[[i]]=nextState[If[i==1,sentinel,seq[[i-1]]],seq[[i]],If[i==n,sentinel,new[[i+1]]]],{i,n,1,-1}];new];
evolveQuantumFSSP[n_Integer?Positive,maxSteps_Integer?Positive]:=Module[{branches,history={}},branches={ReplacePart[ConstantArray[idle,n],1->"G"]};AppendTo[history,branches];Do[branches=DeleteDuplicates[Flatten[Table[{updateSeqLR[b],updateSeqRL[b]},{b,branches}],1]];AppendTo[history,branches],{maxSteps}];Column[{Style["Quantum-Inspired Firing-Squad ("<>ToString[n]<>" cells, "<>ToString[maxSteps]<>" steps)",14,Bold],Sequence@@Table[Column[{Style["Step "<>ToString[step],12,Bold],GraphicsRow[drawFrame/@history[[step+1]],Spacings->2]}],{step,0,maxSteps}]},Spacings->2]];
Print[Style["Running Deterministic Simulation...",Italic]];
evolveDeterministicFSSP[13]
Print[Style["\nRunning Quantum-Inspired (Multiway) Simulation...",Italic]];
evolveQuantumFSSP[7,6]

This analysis extends our previous work by constructing a cellular automaton model that serves as a formal, one-dimensional intuition for achieving in-order delivery. This model demonstrates the fundamental flaw in conventional networking: the treatment of the network as a passive, "dumb" pipe, which forces endpoints to recover from the resultant chaos of dropped, reordered, and duplicated packets.

The model's use of back-pressure represents a foundational step toward a more intelligent fabric, shifting the responsibility for order and reliability from the endpoints back into the network itself. By employing an agent-based simulation, we can cleanly model these dynamics. This approach greatly simplifies the task of specifying and verifying our architecture, whether we are making the case for reliable atomic links or defining the behavior of our local cell-based emulation framework.

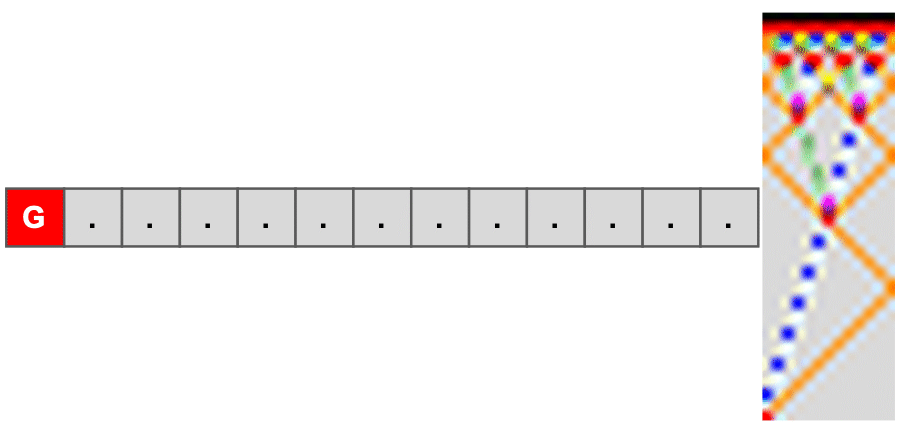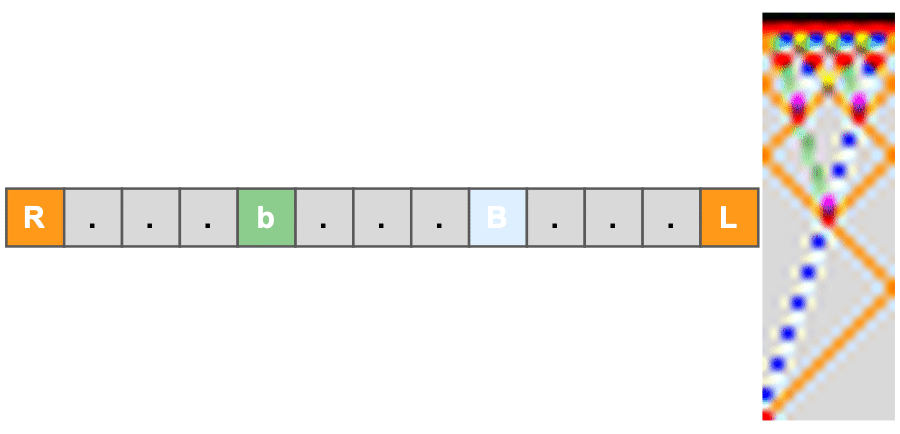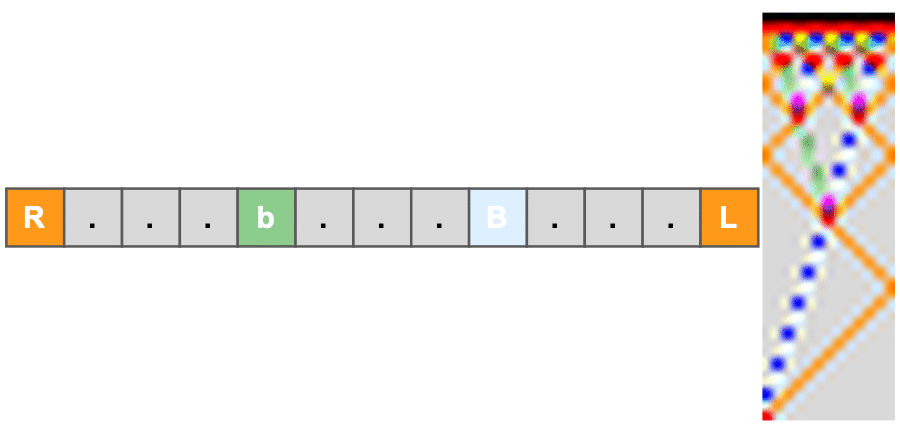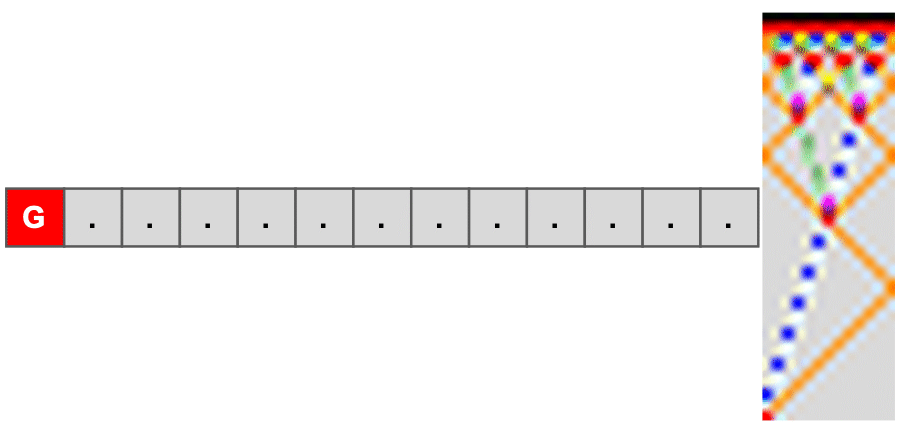
Our model constructs a multiway evolution by generating two possible next states at each step: one derived from a left-to-right update sweep and the other from a right-to-left sweep. This process creates a branching tree of all possible causal histories.

Simulating Indefinite Causal Order

It is crucial to note that this is not a simulation of quantum physics itself, but rather a powerful classical model of a system exhibiting indefinite causal order. This multiway evolution directly visualizes the causality paradox inherent in unreliable networks. When a node receives messages out of order, it is faced with a choice that leads to divergent, branching causal histories.

The Fragmentation of Causal History

As shown in our work with the Open Atomic Ethernet project, the system effectively exists in a superposition of states, where the precise causal order of events remains indefinite until an observation or a specific protocol action forces a collapse to a single history. The branching nature of this evolution demonstrates a fundamental truth: the single, definite causal order assumed by logical timestamp systems inevitably fragments into multiple incompatible histories when confronted with the realities of an asynchronous, unreliable fabric.

ClearAll["Global`*"];
stateToInt=Association["\[CenterDot]"->0,"G"->1,"L"->2,"R"->3,"A"->4,"B"->5,"C"->6,"a"->7,"b"->8,"c"->9,"bB"->10,"cC"->11,"RL"->12,"LR"->13,"F"->14];
intToState=Association[KeyValueMap[#2->#1&,stateToInt]];
nextState[l_String,s_String,r_String]:=Module[{lLast=StringTake[l,-1],rFirst=StringTake[r,1]},Which[s=="A",If[rFirst=="L","G","B"],s=="B","C",s=="C",If[rFirst=="L","G","\[CenterDot]"],s=="a",If[lLast=="R","G","b"],s=="b","c",s=="c",If[lLast=="R","G","\[CenterDot]"],s=="bB","cC",s=="cC",If[lLast=="R"||rFirst=="L","G","\[CenterDot]"],s=="G",Which[MemberQ[{"$$","$G","G$","GG"},l<>r],"F",r=="\[CenterDot]"&&l=="\[CenterDot]","bB",r=="\[CenterDot]","B",l=="\[CenterDot]","b",True,"G"],s=="L",Which[l=="$"||lLast=="R","R",lLast=="C","G",r=="G","L",True,"\[CenterDot]"],s=="R",Which[r=="$"||rFirst=="L","L",rFirst=="c","G",True,"\[CenterDot]"],s=="LR",If[lLast=="C"||rFirst=="c","G","\[CenterDot]"],s=="RL","LR",s=="\[CenterDot]",Which[(l=="G"||lLast=="R")&&(r=="G"||rFirst=="L"),"RL",l=="G"||lLast=="R","R",r=="G"||rFirst=="L","L",lLast=="C","A",rFirst=="c","a",True,"\[CenterDot]"],True,s]];
simulateFiringSquad[n_:21,maxSteps_:60]:=Module[{seq=ConstantArray["\[CenterDot]",n],history={},newSeq},seq[[1]]="G";AppendTo[history,seq];Do[newSeq=Table[With[{l=If[j==1,"$",seq[[j-1]]],r=If[j==n,"$",seq[[j+1]]]},nextState[l,seq[[j]],r]],{j,n}];AppendTo[history,newSeq];seq=newSeq;If[Union[seq]=={"F"},Break[]],{maxSteps}];history];
palette=ColorData["Rainbow"]/@Subdivide[0,1,14];
colorRules=Thread[Range[0,14]->palette];
firingSquadAnimate[n_:21,max_:60]:=Module[{hist=simulateFiringSquad[n,max]/. stateToInt},ListAnimate[(ArrayPlot[hist[[1;;#1]],ColorRules->colorRules,Frame->False,PixelConstrained->8,ImageSize->Large]&)/@Range[Length[hist]],AnimationRunning->False,AnimationRepetitions->1,DefaultDuration->0.25 Length[hist]]];
firingSquadAnimate[21,60]

The central challenge in distributed systems is achieving reliable synchronization when faced with a branching, uncertain graph of causal possibilities. Conventional solutions attempt to solve this by forcing a single, linear timeline through global consensus protocols, but this approach is inherently brittle, slow, and does not scale.

Pruning Causal Histories with Reversible Subtransactions

The DÆDÆLUS methodology offers a different path. Instead of forcing global agreement, we embrace the multiway graph of all possible causal histories and provide a mechanism to prune inconsistent branches safely and locally.

If a sequence of operations along one branch leads to an inconsistent or undesirable state—a causal phantom—the transaction can be reversed. This unwinds the state changes precisely without a global rollback, allowing the system to prune inconsistent branches of the multiway graph locally and safely.

Practical Implications

This methodology has direct implications for structuring systems like Git and iCloud, where file synchronization issues and filesystem corruption often stem from the inability to cleanly resolve divergent states. By providing a framework for local, reversible state changes, we can build systems that are not only scalable but also fundamentally more resilient to the inconsistencies that plague conventional synchronization models.

The primary methodology for formalizing understanding is the use of computational language. A principal example of this is the Wolfram Language. This approach requires one to take a conceptual understanding, formalize it in precise computational terms, and then execute it to observe its consequences. This process often reveals unexpected behaviors that fundamentally refine the original understanding.

Historically, algorithms were engineered by humans; more recently, they are learned from data through progressive adaptation. We are pursuing a different approach: mining the computational universe for novel algorithms. Exhaustive searches within this universe consistently yield more unexpected and often more minimal results than incremental methods. The work presented here is a case in point, demonstrating the power of this methodology in practice.

Module[{starCount = 2500, sceneR = 10, lineY = 4, 
  presentBox = {0.8, 0.8}, swirlShift = -2, swirlR = 5, stars, 
  timeline, swirl, frame, labels, quote}, 
 stars = {White, PointSize[Tiny], 
   Point[RandomPoint[Disk[{0, 0}, sceneR], starCount]]}; 
 timeline = 
  Module[{ticks = Range[-8, 8, 2], years}, 
   years = 1950 + (ticks + 8) 25; 
   Flatten[{White, Thickness[.004], Line[{{-8, lineY}, {8, lineY}}], 
     Table[{Line[{{x, lineY - .2}, {x, lineY + .2}}], 
       If[EvenQ[i], 
        Text[Style[ToString[years[[i + 1]]], 9, White], {x, 
          lineY - .6}]]}, {i, 0, 
       Length[ticks] - 1}, {x, {ticks[[i + 1]]}}], 
     Table[Text[
       Style[If[EvenQ[k], "cause", "effect"], 9, 
        White], {ticks[[k + 1]], lineY + 0.8}], {k, 0, 
       Length[ticks] - 1}], {Cyan, 
      Rectangle[{-(presentBox[[1]]/2), lineY + .25}, {presentBox[[1]]/
        2, lineY + .25 + presentBox[[2]]}]}, 
     Text[Style["Present", 13, White], {0, lineY + 1.3}], 
     Text[Style["Past", 11, White], {-8, lineY - 1}], 
     Text[Style["Future", 11, White], {8, lineY - 1}]}]]; 
 swirl = Module[{a = .05, b = .045, \[Theta]max = 24, 
    d\[Theta] = .05, \[Phi]list}, \[Phi]list = 
    Range[0, 2 \[Pi] - \[Pi]/8, \[Pi]/8]; 
   Table[Line[
     Table[With[{r = a Exp[b \[Theta]]}, 
       r {Cos[\[Theta] + \[Phi]], Sin[\[Theta] + \[Phi]]}], {\[Theta],
        0, \[Theta]max, d\[Theta]}]], {\[Phi], \[Phi]list}]]; 
 frame = {White, Opacity[.5], Circle[{0, 0}, swirlR]}; 
 labels = 
  Table[With[{\[Theta] = (2 \[Pi] k)/8, 
     tag = If[EvenQ[k], "cause", "effect"]}, 
    Text[Style[tag, 10, 
      White], (swirlR + 1) {Cos[\[Theta]], Sin[\[Theta]]}]], {k, 0, 
    7}]; quote = {Text[
    Style["People assume that time is a strict progression of cause \
to effect, but actually, from a non-linear,\n non-subjective \
viewpoint, it's more like a big ball of wibbly-wobbly\[Ellipsis] \
timey-wimey\[Ellipsis] stuff.", 12, White, LineSpacing -> {1.2, 0}, 
     TextJustification -> .5], {0, -7.3}, Center], 
   Text[Style["\[LongDash] The Doctor", 11, White, 
     Italic], {0, -8.2}]}; 
 Graphics[{Black, Rectangle[{-sceneR, -sceneR}, {sceneR, sceneR}], 
   stars, timeline, Translate[swirl, {0, swirlShift}], 
   Translate[frame, {0, swirlShift}], 
   Translate[labels, {0, swirlShift}], quote}, 
  PlotRange -> {{-sceneR, sceneR}, {-sceneR, sceneR}}, 
  Background -> Black, ImageSize -> 600]]

The foundational insight of our work is the principle of reversibility: it is more robust to reverse a sequence of small, intermediate steps than to attempt to resolve a consistent global state in a single, complex operation. This "reversibility logic" is at the heart of the Æ-Link instruction set and is embedded within all of our scouting and routing algorithms.

We utilize Mathematica as our primary tool for formalizing this principle. It serves as a comprehensive language for specification, configuration, and simulation, allowing us to model the fundamental physics of information flow. Our work on the Distributed Firing Squad Problem prepares us for this, framing the challenges of time, clocks, and event reordering that these models must solve.

The Root of the Problem: The Façade of Newtonianism

This approach is necessary because the fundamental issue plaguing modern distributed systems is the façade of Newtonianism. The assumption of a single, global, irreversible timeline is a flawed abstraction that leads to systemic, cascading failures.

Case Study: Git and iCloud Synchronization

The consequences of this flawed assumption are not theoretical; they manifest as persistent file synchronization corruption in widely used systems like Git and iCloud. The diamond structures that appear in a Git commit graph upon a merge are a direct visualization of divergent causal histories. Subsequent synchronization conflicts are often misdiagnosed, but they are symptoms of a deeper atomicity problem rooted in the unreliable, best-effort assumptions of the underlying Ethernet fabric. This is a manifestation of the "Ethernet Spacetime" misunderstanding that pervades modern infrastructure at Apple, AWS, and Google alike.

The evolution from the deterministic Firing Squad Problem (FSSP) to a multiway FSSP mirrors the paradigm shift from classical networking to the DÆDÆLUS architecture. We do not solve the problem of causal uncertainty by eliminating it with fragile global assumptions; rather, we provide the tools to navigate through it with local, verifiable, and reversible operations. Our objective is to produce modular components and high-level, human-readable code that makes each part of this complex system understandable on its own.

Modeling the Classic Ether

To ground this paradigm, we are developing a specific, agent-based model of the classic Ethernet. Initially focusing on a bidirectional, acknowledged data flow, the model is designed to replicate the packet transmission mechanics described in Metcalfe's seminal paper. While the statistical analysis from that work serves as a validation target, our primary objective is to create a clean, step-by-step simulation of the transmission process itself.

Simulation Architecture and Event Logging

The simulation is architected with the following principles:

• Discrete, Integer-Based Time: Time advances in discrete integer steps, ensuring deterministic and repeatable behavior.
• Atomic Event Processing: To handle events occurring at the same logical time, the simulation processes all simultaneous events before advancing the clock, ensuring consistency.
• Per-Link State Machine: The link is the fundamental unit of serialization and is modeled as a state machine with discrete states: IDLE, BUSY, COLLISION, or JAM.

• Event Log Output: The primary output is a per-link event log that records every packet transmission and state change. These logs are designed to be replayed, enabling the visualization of packet flows, collisions, and the creation of precise timeline diagrams.

  DynamicModule[{symbols={"CHERRY","GRAPE","LEMON","WATERMELON","ORANGE"},values=Association["CHERRY"->10,"GRAPE"->20,"LEMON"->30,"WATERMELON"->40,"ORANGE"->60],reelFinals,spinStart,spinning=False,godMode=False,winnings=0},reelFinals=ConstantArray["",3];spinStart=0;Deploy[Column[{Style["THE SLOTS",34,FontFamily->"Bebas Neue"],Spacer[20],Row[Table[With[{ii=ii},Dynamic[Style[If[spinning&&AbsoluteTime[]-spinStart<1.6,RandomChoice[symbols],reelFinals[[ii]]],FontSize->24],UpdateInterval->0.05]],{ii,1,3}],Spacer[20]],Spacer[20],Row[{Button["Spin",If[!spinning,spinning=True;spinStart=AbsoluteTime[];RunScheduledTask[reelFinals=Table[RandomChoice[symbols],{3}];If[godMode,reelFinals=ConstantArray[First[reelFinals],3];];If[Length[Union[reelFinals]]==1,winnings+=values[reelFinals[[1]]]];spinning=False;,{1.6,1}];],ImageSize->{80,40}],Spacer[20],Button["God's Eye",godMode=!godMode,Appearance->Dynamic[If[godMode,"Pressed","Normal"]],ImageSize->{80,40}]}],Spacer[20],Dynamic[Style["Winnings: "<>ToString[winnings],20]]},Alignment->Center]]]
  

Replaying per-link event logs synchronously to achieve a cohesive, system-wide view requires a Global Timeframe. Within the simulation's "God's eye view," events on different links that share the same discrete integer timestamp are considered to have occurred simultaneously.

A Hybrid Simulation Architecture

To achieve this, we propose a hybrid simulation architecture that leverages the strengths of both Python and Mathematica. Rather than a purely symbolic approach, this pragmatic methodology uses Python for the core simulation and Mathematica for analysis and visualization.

• The Simulation Engine (Python): The core agent-based simulation will be implemented in Python to leverage its robust ecosystem. We can use libraries like PyTransitions to formally define the link state machines (IDLE, BUSY, COLLISION, JAM). This allows us to model packet metadata (e.g., source, destination, ACK type) without simulating the exact bit patterns, focusing on the protocol's logical behavior. A Python foundation provides a clear path to scale the model from the initial half-duplex channel to more complex full-duplex and even Aloha-style contention systems.
• The Analysis & Visualization Engine (Mathematica): The Python simulation will export detailed event logs as its primary artifact. These logs can then be imported into Mathematica to render precise timeline diagrams of link states and replay complex event sequences, such as packet collisions. This maintains our "code-as-proof" methodology, using the simulation output for formal analysis.

This hybrid approach allows for rapid development by leveraging existing Python libraries while reserving Mathematica for its unparalleled strengths in formal analysis and visualization. It offers the most pragmatic and scalable path forward.

The greatest challenge in distributed computing is not merely delivering data, but synchronizing action across multiple nodes in the face of causal ambiguity. The classic Firing Squad Synchronization Problem (FSSP) serves as a computational parable for this challenge, defining the problem of achieving simultaneous action among distributed agents. The classical FSSP assumes a deterministic world where a single, correct timeline can be established through an orchestrated exchange of signals, reflecting the conventional approach to networking that seeks to impose a single causal history on an inherently unpredictable system.

The DÆDÆLUS paradigm reframes this problem from a multiway perspective. We begin with the system in an inert, inactivated state where causal relationships are yet to be defined. Instead of forcing a single outcome, our model allows the system to evolve into a causal superposition—a branching graph of all possible histories. This approach is not a direct simulation of quantum physics but a powerful, quantum-inspired model for systems with indefinite causal order.

This journey from a deterministic FSSP to a multiway FSSP illustrates the fundamental departure of our methodology. We do not solve for a single, globally consistent state; instead, we provide the tools to navigate the multiway graph of possibilities. Our cellular automaton model for reliable delivery is built on this foundation, ensuring that a packet is either verifiably delivered or its failure is explicitly known, thereby pruning impossible branches from the causal tree.

DynamicModule[{$happenedBeforeMatrix, $events = 
   CharacterRange["A", "Z"], 
  colorRules = {1 -> White, -1 -> White, 0 -> Black}, examples, 
  resetGVM, insertLogic, processCommands, rebuild}, 
 examples = 
  Association[
   "Linear Chain" -> 
    StringRiffle[
     Table["insert " <> $events[[i]] <> "->" <> $events[[i + 1]], {i, 
       1, 25}], "; "], 
   "Diamond Shape" -> 
    "insert A->B; insert A->C; insert B->D; insert C->D; insert D->E; \
insert E->F; insert E->G; insert F->H; insert G->H; insert H->I; \
insert I->J; insert I->K; insert J->L; insert K->L; insert L->M; \
insert M->N; insert M->O; insert N->P; insert O->P; insert P->Q; \
insert Q->R; insert Q->S; insert R->T; insert S->T; insert T->U; \
insert U->V; insert U->W; insert V->X; insert W->X; insert X->Y; \
insert Y->Z;", 
   "Fork-Join" -> 
    "insert A->B; insert A->C; insert A->D; insert B->E; insert C->E; \
insert D->E; insert E->F; insert F->G; insert F->H; insert G->I; \
insert H->I; insert I->J; insert J->K; insert J->L; insert J->M; \
insert K->N; insert L->N; insert M->N; insert N->O; insert O->P; \
insert O->Q; insert P->R; insert Q->R; insert R->S; insert S->T; \
insert S->U; insert S->V; insert T->W; insert U->W; insert V->W; \
insert W->X; insert X->Y; insert Y->Z;", 
   "Parallel Streams" -> 
    "insert A->B; insert C->D; insert E->F; insert G->H; insert I->J; \
insert K->L; insert M->N; insert O->P; insert Q->R; insert S->T; \
insert U->V; insert W->X; insert Y->Z;", 
   "Random DAG" -> 
    "insert A->D; insert A->C; insert B->D; insert B->E; insert C->F; \
insert D->G; insert E->H; insert F->H; insert G->I; insert H->J; \
insert I->K; insert J->K; insert K->L; insert L->M; insert L->N; \
insert M->O; insert N->P; insert O->Q; insert P->Q; insert Q->R; \
insert R->S; insert S->T; insert T->U; insert U->V; insert V->W; \
insert W->X; insert X->Y; insert Y->Z;", 
   "Simple Cycle" -> 
    "insert A->B; insert B->C; insert C->D; insert D->E; insert E->F; \
insert F->G; insert G->H; insert H->I; insert I->J; insert J->K; \
insert K->L; insert L->M; insert M->N; insert N->O; insert O->P; \
insert P->Q; insert Q->R; insert R->S; insert S->T; insert T->U; \
insert U->V; insert V->W; insert W->X; insert X->Y; insert Y->Z; \
insert Z->A;"]; 
 resetGVM[] := ($happenedBeforeMatrix = 
     ConstantArray[0, {Length[$events], Length[$events]}];); 
 insertLogic[eA_String, eB_String] := 
  Module[{posA, posB, n = Length[$events]}, 
   posA = First[Flatten[Position[$events, eA]]]; 
   posB = First[Flatten[Position[$events, eB]]]; 
   If[$happenedBeforeMatrix[[posB, posA]] === 1, 
    Return[]]; $happenedBeforeMatrix[[posA, posB]] = 
    1; $happenedBeforeMatrix[[posB, posA]] = -1; 
   Do[If[$happenedBeforeMatrix[[k, posA]] === 
       1 && $happenedBeforeMatrix[[k, posB]] =!= 
       1, $happenedBeforeMatrix[[k, posB]] = 
      1; $happenedBeforeMatrix[[posB, k]] = -1;], {k, n}]; 
   Do[If[$happenedBeforeMatrix[[posB, k]] === 
       1 && $happenedBeforeMatrix[[posA, k]] =!= 
       1, $happenedBeforeMatrix[[posA, k]] = 
      1; $happenedBeforeMatrix[[k, posA]] = -1;], {k, n}];]; 
 processCommands[txt_String] := 
  Module[{parts}, parts = StringSplit[txt, ";"]; 
   Do[With[{c = StringTrim[part]}, 
     If[StringStartsQ[c, "insert"], 
      Module[{ev = StringSplit[StringTrim[StringDrop[c, 6]], "->"]}, 
       If[Length[ev] == 2, insertLogic[ev[[1]], ev[[2]]]]]]], {part, 
     parts}];]; 
 rebuild[] := 
  Module[{edges, Gfull, Gred, fullPlot, hassePlot}, 
   edges = Flatten[
     Table[If[$happenedBeforeMatrix[[i, j]] === 
        1, $events[[i]] -> $events[[j]], Nothing], {i, 
       Length[$events]}, {j, Length[$events]}]]; 
   Gfull = Graph[$events, edges, DirectedEdges -> True]; 
   Gred = TransitiveReductionGraph[Gfull]; 
   fullPlot = 
    GraphPlot[edges, DirectedEdges -> True, 
     VertexRenderingFunction -> ({Black, Disk[#1, 0.025], Black, 
         Text[#2, #1]} &), PlotStyle -> {RGBColor[0, 0, 0.5]}, 
     ImageSize -> {300, 250}]; 
   hassePlot = 
    GraphPlot[EdgeList[Gred] /. x_ \[DirectedEdge] y_ :> x -> y, 
     DirectedEdges -> True, 
     VertexRenderingFunction -> ({Black, Disk[#1, 0.025], Black, 
         Text[#2, #1]} &), PlotStyle -> {RGBColor[0, 0, 0.5]}, 
     ImageSize -> {300, 250}]; 
   Column[{fullPlot, Spacer[10], hassePlot}]]; 
 Column[Table[resetGVM[]; processCommands[examples[exName]]; 
   Framed[Column[{Style[exName, Black, Bold, 16], Spacer[5], 
      rebuild[], Spacer[10], 
      MatrixPlot[$happenedBeforeMatrix, ColorRules -> colorRules, 
       Mesh -> All, Frame -> True, 
       FrameTicks -> {Table[{i, Style[$events[[i]], Black, 10]}, {i, 
           Length[$events]}], 
         Table[{j, Style[$events[[j]], Black, 10]}, {j, 
           Length[$events]}]}, FrameTicksStyle -> Black, 
       ImageSize -> {500, 450}, Background -> White]}], 
    Background -> White, FrameStyle -> Black, 
    RoundingRadius -> 6], {exName, Keys[examples]}], Spacings -> 2]]

The evolveDeterministicFSSP function simulates the classical Firing Squad Synchronization Problem (FSSP). The simulation begins with a command from a single "General," initiating a sequence of signal propagations that reflect and interact until all "soldiers" fire simultaneously. The resulting space-time diagram reveals a single, predictable causal history.

This simulation is a perfect embodiment of the Forward-In-Time-Only (FITO) fallacy that underpins conventional distributed systems. It is built on a set of computationally convenient but flawed assumptions: a single, definite causal order that is globally consistent and irreversible.

This deterministic model is fundamentally fragile because it systematically conflicts with both relativistic physics and practical network constraints. The quest for a single, consistent timeline collides with physical reality, which does not provide a universal "now". Real-world networks, with their variable latencies, non-uniform topologies, and failure modes, violate the basic assumptions that make deterministic synchronization possible. Ultimately, you cannot synchronize clocks the way you think, and any model that relies on this illusion is destined to fail when confronted with physical reality.

We present DynamicNetworks, a Mathematica-based simulation toolkit for interactively modeling and visualizing packet networks. The framework reproduces phenomena from early protocols like ALOHA and 1970s Ethernet—such as collision domains and retransmission timing—and extends to modern Clos networks and experimental systems like Open Atomic Ethernet, enabling direct experimentation with deterministic multicast and atomic commit semantics. Our tools emphasize time-evolving visualizations and real-time parameter tuning to bridge the gap between textbook theory and live systems intuition.

A key question is whether this simulator can be merged with the DÆDÆLUS Emulator. The primary incompatibility lies in the simulator's reliance on a global ordering of events to synchronize transmissions—a construct our architecture explicitly rejects. A potential path forward involves developing a synchronization mechanism for the per-link logs generated by the emulator. These logs could then be replayed and visualized in Mathematica, replacing the global priority queue with a model grounded in the emulator's local, asynchronous reality. As computer engineers for DÆDÆLUS and project leads for Atomic Ethernet, we are interested in the fuzzy line between hardware and software, and in making small changes at the base of the tower that ripple all the way to the top.

Causality as Computation: From Lamport's Logic to the Graph Virtual Machine

The Firing Squad Problem highlights the challenge of synchronizing action in time, but the more fundamental problem is ordering the events themselves. To this end, we have developed an elegant, executable specification of Lamport's "happens-before" relation—the foundational logic for establishing causality in classical distributed systems.

At the heart of this simulation is the insertLogic function. When a new causal link is introduced, the code computes the transitive closure of the entire system. This creates a mathematically consistent partial order, but it relies on an illusion of global knowledge. The resulting causality matrix represents a "God's-eye-view" of the event history, where the implications of a single message are instantly propagated across the entire logical structure.

This model perfectly illustrates the Forward-In-Time-Only (FITO) assumptions that the DÆDÆLUS architecture is designed to transcend. Real systems do not have access to this instantaneous, global truth; they are composed of CELLs connected by LINKs, and each CELL operates from a strictly local perspective.