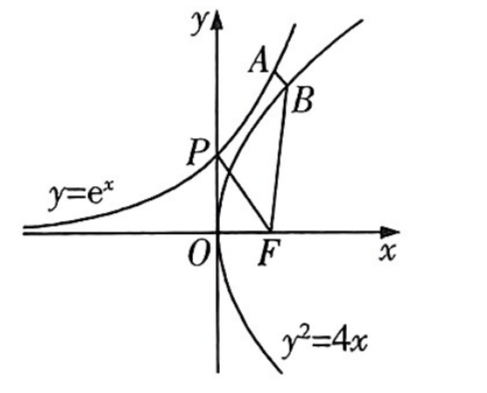
FunctionRange[{y^2/4 + Sqrt[(x - y^2/4)^2 + (E^x - y)^2] + 1}, {x,
y}, t] // Quiet
Run the code above to get this range:
t >= 1.41421
Running the code below does not yield any results.
Minimize[{y^2/4 + Sqrt[(x - y^2/4)^2 + (E^x - y)^2] +
1, {x, y} \[Element] Reals}, {x, y}]
How to Find the Exact Range of a Function Involving Exponential and Quadratic Terms
The manual calculation process is as follows: