There is another thing about the periodic boundary conditions. The examples I showed above lives on a torus due to its periodic boundary conditions. So if you solve the equation
sols = NDSolve[{D[u[x, y, t], {t, 2}] ==
0.1 (D[u[x, y, t], {x, 2}] + D[u[x, y, t], {y, 2}]),
u[x, y, 0] == Sin[2 Pi*(x + y)], D[u[x, y, t], t] == 0 /. t -> 0.,
u[0, y, t] == u[1, y, t], u[x, 0, t] == u[x, 1, t]},
u, {x, 0, 1}, {y, 0, 1}, {t, 0, 12}]
then export the frames:
frames = For[k = 7.5, k <= 9.5, k = k + 0.075,
Export["~/Desktop/Movie/frame" <> ToString[1000*k] <> ".gif",
ParametricPlot3D[{(2 + Cos[v]) Cos[u], (2 + Cos[v]) Sin[u],
Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi}, Mesh -> None,
TextureCoordinateFunction -> ({#1, #2} &), Boxed -> False,
Axes -> False,
PlotStyle ->
Texture[ImageCrop[
Image[ContourPlot[u[x, y, k] /. sols, {x, 0, 1}, {y, 0, 1},
Contours -> 150, ContourLines -> False,
ImagePadding -> False, Frame -> False,
PlotRange -> {-1.1, 1.1},
ColorFunctionScaling -> False]], {{14, 360 - 14}, {14,
360 - 14}}]]]]];
you get something like this:
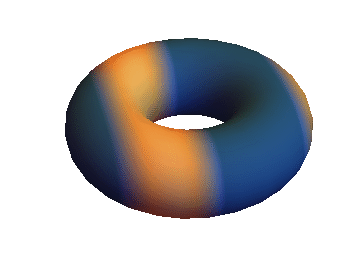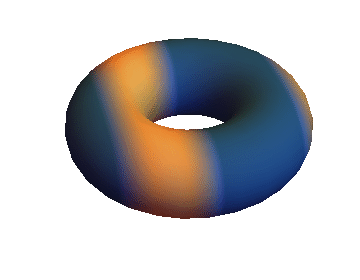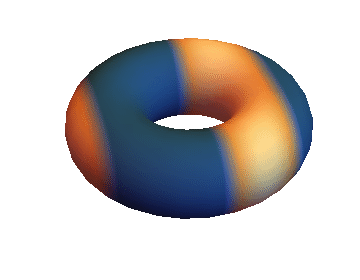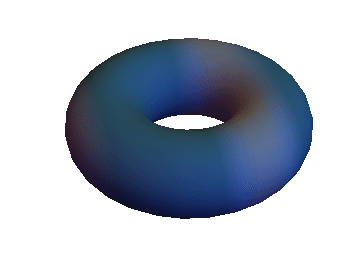
which should actually move.
Cheers,
Marco